Float Compression 7: More Filtering Optimization
Introduction and index of this series is here.
In the previous post I explored how to make data filters a bit faster, using some trivial merging of filters, and a largely misguided attempt at using SIMD.
People smarter than me pointed out that getting good SIMD performance requires a different approach. Which is kinda obvious, and another thing that is obvious is that I have very little SIMD programming experience, and thus very little intuition of what’s a good approach.
But to get there, first I’d need to fix a little poopoo I made.
A tiny accidental thing can prevent future things
Recall how in part 3 the most promising data
filter seemed to be “reorder bytes + delta”? What it does, is first reorder data items so that
all 1st bytes are together, then all 2nd bytes, etc. If we had three items of four bytes each, it
would do this:
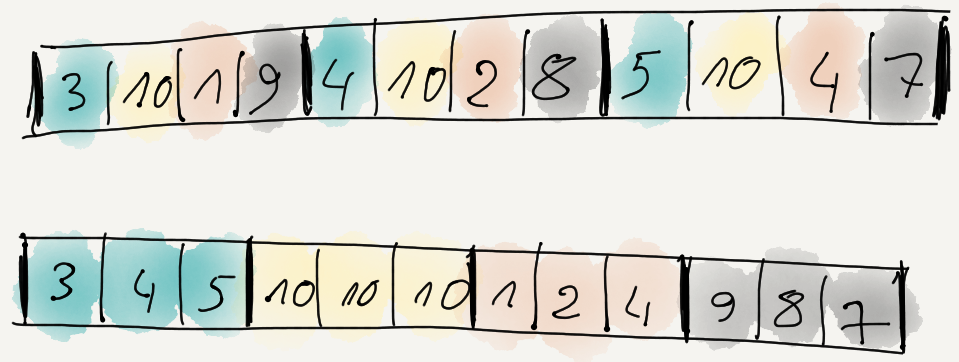
And then delta-encode the whole result:
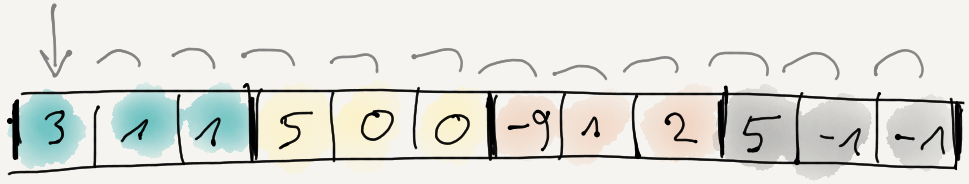
i.e. first byte stays the same, and each following byte is difference from the previous one.
Turns out, this choice prevents some future optimizations. How? Because whole data reordering conceptually produces N separate byte streams, delta-encoding the whole result conceptually merges these streams together; the values in them become dependent on all previous values.
What if instead, we delta-encoded each stream separately?
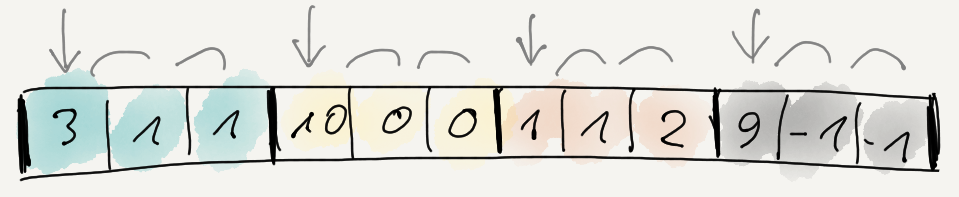
In terms of code, this is a tiny change:
void Split8Delta(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
// uint8_t prev = 0; <-- WAS HERE
for (int ich = 0; ich < channels; ++ich)
{
uint8_t prev = 0; // <-- NOW HERE
const uint8_t* srcPtr = src + ich;
for (size_t ip = 0; ip < dataElems; ++ip)
{
uint8_t v = *srcPtr;
*dst = v - prev;
prev = v;
srcPtr += channels;
dst += 1;
}
}
}
We will see how that is useful later. Meanwhile, this choice of “reorder, then delta the whole result” is what OpenEXR image format also does in the ZIP compression code :)
What the above change allows, is in the filter decoder to fetch from any number of byte streams at once and process their data (apply reverse delta, etc.). Something we could not do before, since values within each stream depended on the values of previous streams.
So, more (questionable) optimizations
Overall I did a dozen experiments, and they are all too boring to write about them here, so here are the main ones.
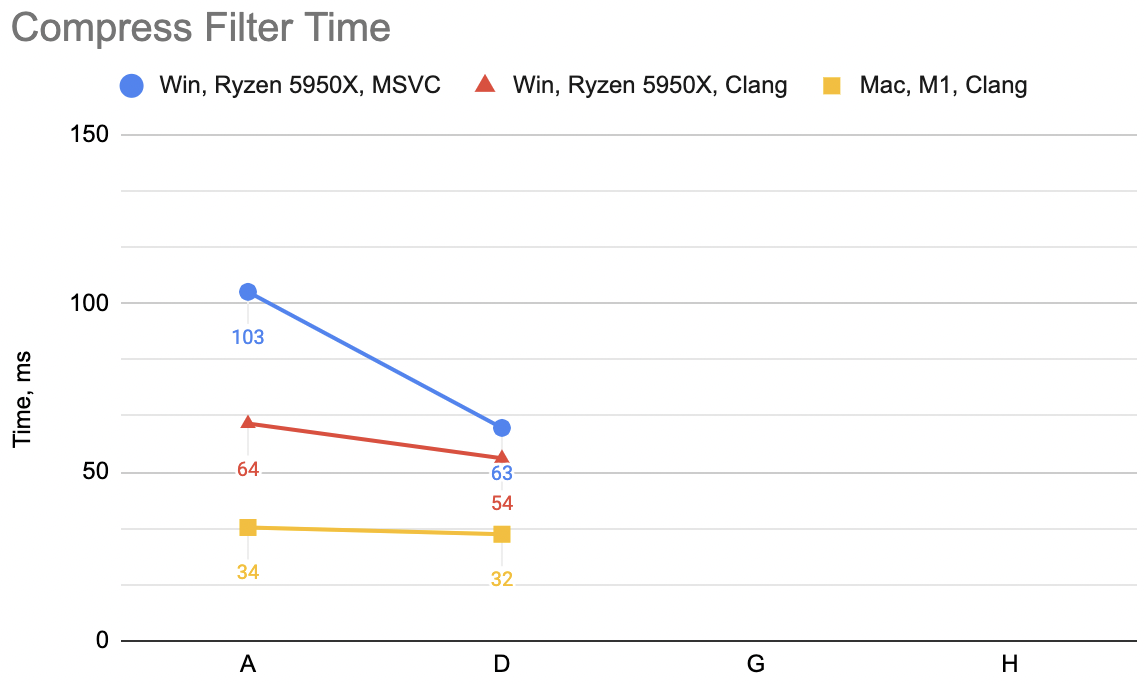
Note: in the previous post I made a mistake in timing calculations, where the time numbers were more like “average time it takes to filter one file”, not “total time it takes to filter whole data set”. Now the numbers are more proper, but don’t directly compare them with the previous post!
In the previous post we went from “A” to “D” variants, resulting
in some speedups depending on the platform (un-filter for decompression: WinVS 106→75ms, WinClang 116→75ms, Mac 94→32ms):
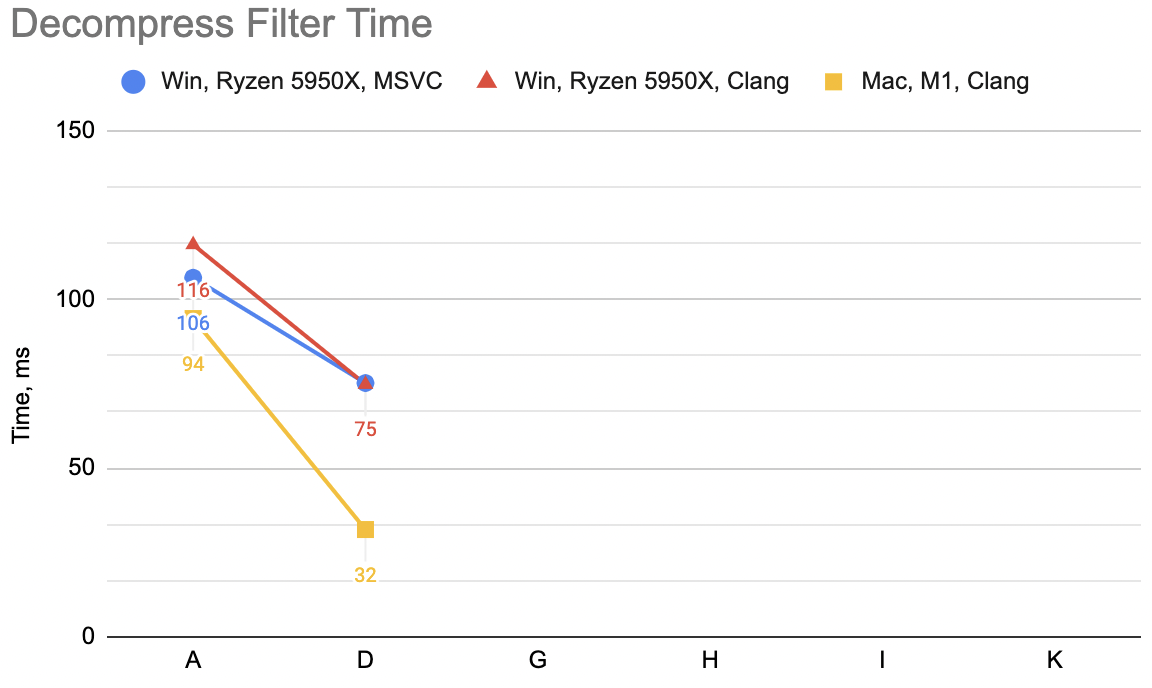
Now that we can decode/unfilter all the byte streams independently, let’s try doing just that (no SIMD at all):
const size_t kMaxChannels = 64;
// Scalar, fetch a byte from N streams, write sequential
void UnFilter_G(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev[kMaxChannels] = {};
uint8_t* dstPtr = dst;
for (size_t ip = 0; ip < dataElems; ++ip)
{
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t v = *srcPtr + prev[ich];
prev[ich] = v;
*dstPtr = v;
srcPtr += dataElems;
dstPtr += 1;
}
}
}
I did hardcode “maximum bytes per data element” to just 64 here. In our data set it’s always either 16 or 12, but let’s make the limit somewhat more realistic. It should be possible to not have a limit with some additional code, but “hey 64 bytes per struct should be enough for anyone”, or so the ancient saying goes.
So this is “G” variant: decompression WinVS 139ms, WinClang 125ms, Mac 104ms (“D” was: 75, 75, 32). This is not great at all! This is way slower! ☹️
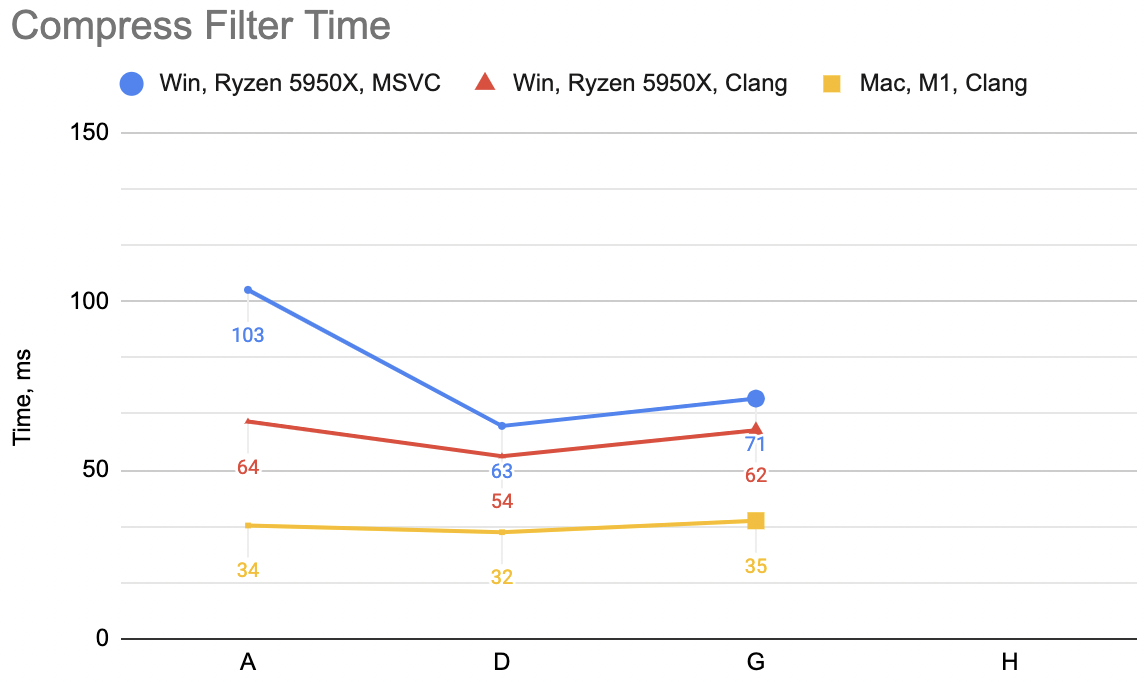
But! See how this fetches a byte from all the “streams” of a data item, and has all the bytes of the previous data item? Doing the “un-delta” step could be done way more efficiently using SIMD now, by processing like 16 bytes at once (128 bit SSE/NEON registers are exactly 16 bytes in size).
A tiny SIMD wrapper, and Transpose
All the SSE and NEON code I scribbled in the previous post felt like I’m just repeating the same things for NEON after doing SSE
part, just with different intrinsic function names. So, perhaps prematurely, I made a little helper to avoid having to
do that: a data type Bytes16 that, well, holds 16 bytes, and then functions like SimdAdd, SimdStore, SimdGetLane and whatnot.
It’s under 100 lines of code, and does just the tiny amount of operations I need:
simd.h.
I will also very soon need a function that transposes a matrix, i.e. flips rows & columns of a rectangular array. As usual, turns out Fabian has written about this a decade ago (Part 1, Part 2). You can cook up a sweet nice 16x16 byte matrix transpose like this:
static void EvenOddInterleave16(const Bytes16* a, Bytes16* b)
{
int bidx = 0;
for (int i = 0; i < 8; ++i)
{
b[bidx] = SimdInterleaveL(a[i], a[i+8]); bidx++; // _mm_unpacklo_epi8 / vzip1q_u8
b[bidx] = SimdInterleaveR(a[i], a[i+8]); bidx++; // _mm_unpackhi_epi8 / vzip2q_u8
}
}
static void Transpose16x16(const Bytes16* a, Bytes16* b)
{
Bytes16 tmp1[16], tmp2[16];
EvenOddInterleave16(a, tmp1);
EvenOddInterleave16(tmp1, tmp2);
EvenOddInterleave16(tmp2, tmp1);
EvenOddInterleave16(tmp1, b);
}
and then have a more generic Transpose function for any NxM sized matrix, with the faster SIMD code path for cases like “16 rows, multiple-of-16 columns”. Why? We’ll need it soon :)
Continuing with optimizations
The “G” variant fetched one byte from each stream/channel, did <something else>, and then fetched the following byte from each stream, and so on. Now, fetching bytes one by one is probably wasteful.
What we could do instead, for the un-filter: from each stream, fetch 16 (SIMD register size) bytes, and decode the deltas
using SIMD prefix sum (very much like in “D” variant). Now we have 16 data items on stack, but they are still in the “split bytes”
memory layout. But, doing a matrix transpose gets them into exactly the layout we need, and we can just blast that into destination
buffer with a single memcpy.
// Fetch 16b from N streams, prefix sum SIMD undelta, transpose, sequential write 16xN chunk.
void UnFilter_H(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t* dstPtr = dst;
int64_t ip = 0;
// simd loop: fetch 16 bytes from each stream
Bytes16 curr[kMaxChannels] = {};
const Bytes16 hibyte = SimdSet1(15);
for (; ip < int64_t(dataElems) - 15; ip += 16)
{
// fetch 16 bytes from each channel, prefix-sum un-delta
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < channels; ++ich)
{
Bytes16 v = SimdLoad(srcPtr);
// un-delta via prefix sum
curr[ich] = SimdAdd(SimdPrefixSum(v), SimdShuffle(curr[ich], hibyte));
srcPtr += dataElems;
}
// now transpose 16xChannels matrix
uint8_t currT[kMaxChannels * 16];
Transpose((const uint8_t*)curr, currT, 16, channels);
// and store into destination
memcpy(dstPtr, currT, 16 * channels);
dstPtr += 16 * channels;
}
// any remaining leftover
if (ip < int64_t(dataElems))
{
uint8_t curr1[kMaxChannels];
for (int ich = 0; ich < channels; ++ich)
curr1[ich] = SimdGetLane<15>(curr[ich]);
for (; ip < int64_t(dataElems); ip++)
{
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t v = *srcPtr + curr1[ich];
curr1[ich] = v;
*dstPtr = v;
srcPtr += dataElems;
dstPtr += 1;
}
}
}
}
The code is getting more complex! But conceptually it’s not – half of the function is the SIMD loop that reads 16 bytes from each channel; and the remaining half of the function is non-SIMD code to handle any leftover in case data size was not multiple of 16.
For the compression filter it is similar idea, just the other way around: read 16 N-sized items from the source data, transpose which gets them into N channels with 16 bytes each. Now do the delta encoding with SIMD on that. Store each of these 16 bytes into N separate locations. Again half of the code is just for handling non-multiple-of-16 data size leftovers.
// Fetch 16 N-sized items, transpose, SIMD delta, write N separate 16-sized items
void Filter_H(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t* dstPtr = dst;
int64_t ip = 0;
const uint8_t* srcPtr = src;
// simd loop
Bytes16 prev[kMaxChannels] = {};
for (; ip < int64_t(dataElems) - 15; ip += 16)
{
// fetch 16 data items
uint8_t curr[kMaxChannels * 16];
memcpy(curr, srcPtr, channels * 16);
srcPtr += channels * 16;
// transpose so we have 16 bytes for each channel
Bytes16 currT[kMaxChannels];
Transpose(curr, (uint8_t*)currT, channels, 16);
// delta within each channel, store
for (int ich = 0; ich < channels; ++ich)
{
Bytes16 v = currT[ich];
Bytes16 delta = SimdSub(v, SimdConcat<15>(v, prev[ich]));
SimdStore(dstPtr + dataElems * ich, delta);
prev[ich] = v;
}
dstPtr += 16;
}
// any remaining leftover
if (ip < int64_t(dataElems))
{
uint8_t prev1[kMaxChannels];
for (int ich = 0; ich < channels; ++ich)
prev1[ich] = SimdGetLane<15>(prev[ich]);
for (; ip < int64_t(dataElems); ip++)
{
for (int ich = 0; ich < channels; ++ich)
{
uint8_t v = *srcPtr;
srcPtr++;
dstPtr[dataElems * ich] = v - prev1[ich];
prev1[ich] = v;
}
dstPtr++;
}
}
}
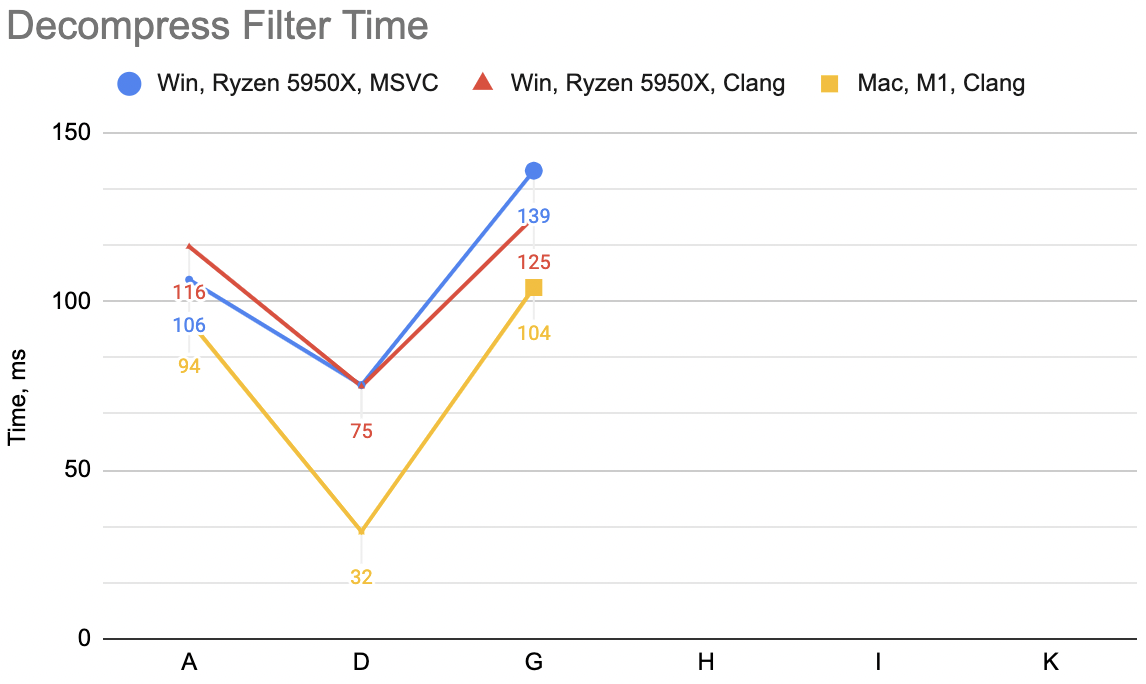
Now that is a lot of code indeed, relatively speaking. Was it worth it? This is variant “H”: decompression unfilter
WinVS 21ms, WinClang 20ms, Mac 28ms (previous best “D” was 75, 75, 32). Compression filter WinVS 24ms,
WinClang 23ms, Mac 31ms (“D” was 63, 54, 32).
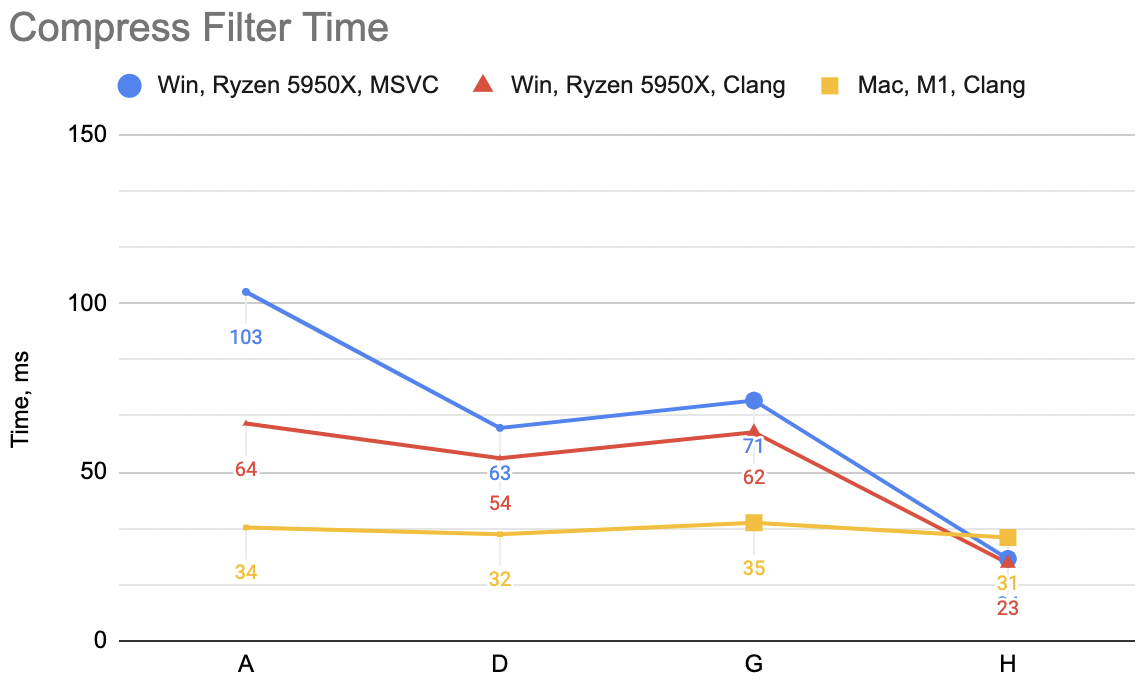
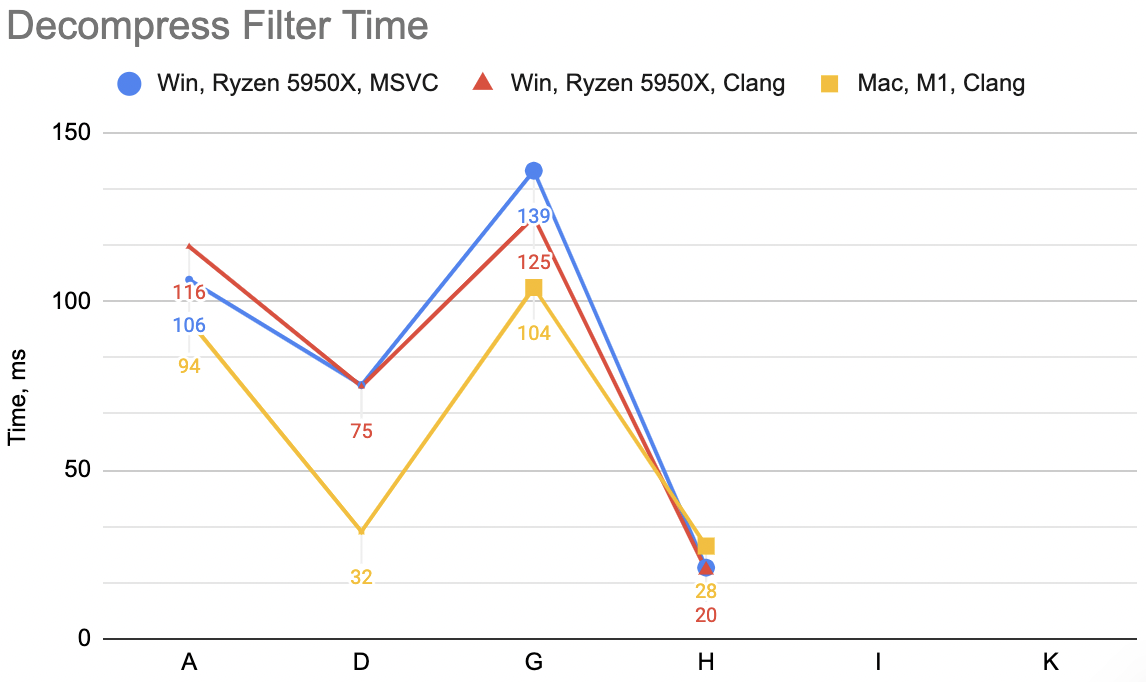
Hey look, not bad at all!
Is it cheating if you optimize for your data?
Next up is a step I did only for the decoding unfilter. It’s not all that interesting, but raises a good question: is it “cheating”, if you optimize/specialize your code for your data?
The answer is, of course, “it depends”. In my particular case, I’m testing on four data files, and three of them use
data items that are 16 bytes in size (the 4th one uses 12 byte items). The UnFilter_H function above is written
for generic “any, as long as <64 bytes item size” data. What I used that exact code for all non-16 sized data, but
did “something better” for 16-sized data?
In particular, the transpose step becomes exact 16x16 matrix transpose, for which we have a sweet nice function already. And the delta decoding could be done after the transpose, using way more efficient “just add SIMD registers” operation instead of trying to cram that into SIMD prefix sum. The interesting part of the SIMD inner loop becomes this then:
// fetch 16 bytes from each channel
Bytes16 curr[16];
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < 16; ++ich)
{
Bytes16 v = SimdLoad(srcPtr);
curr[ich] = v;
srcPtr += dataElems;
}
// transpose 16xChannels matrix
Bytes16 currT[16];
Transpose((const uint8_t*)curr, (uint8_t*)currT, 16, channels);
// un-delta and store
for (int ib = 0; ib < 16; ++ib)
{
prev = SimdAdd(prev, currT[ib]);
SimdStore(dstPtr, prev);
dstPtr += 16;
}
Does that help? “I” case: decompression unfilter WinVS 18ms, WinClang 14ms, Mac 24ms (“H” was 21, 20, 28). Yeah, it does help.
Groups of four
Fabian pointed out that fetching from “lots” (e.g. 16) separate streams at once can get into an issue of CPU cache trashing. If the streams spaced apart at particular powers of two, and you are fetching from more than 4 or 8 (typical CPU cache associativity) streams at once, it’s quite likely that many of your memory fetches will be landing into the same physical CPU cache lines.
One possible way to avoid this is also “kinda cheating” (or well, “using knowledge of our data”) – we know we are operating on floating point (4-byte) things, i.e. our data structure sizes are always a multiple of four. We could be fetching not all N (N = data item size) streams at once, but rather do that in groups of 4 streams. Why four? Because we know the number of streams is multiple of four, and most CPU caches are at least 4-way associative.
So conceptually, decompression unfilter would be like (straight pseudo-code paste from Fabian’s toot):
for (chunks of N elements) {
for groups of 4 streams {
read and interleave N values from 4 streams each
store to stack
}
for elements {
read and interleave groups of 4 streams from stack
sum into running total
store to dest
}
}
This hopefully avoids some CPU cache trashing, and also fetches more than 16 bytes from each stream in one go. Ideally we’d want to fetch as much as possible, while making sure that everything we’re working with stays in CPU L1 cache.
I’ve tried various sizes, and in my testing size of 384 bytes per channel worked best. The code is long though, and kind of a mess; the “we effectively achieve a matrix transpose, but in two separate steps” is not immediately clear at all (or not clear at my lacking experience level :)). In the code I have separate path for 16-sized data items, where the 2nd interleave part is much simpler.
Anyhoo, here it is:
void UnFilter_K(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
assert((channels % 4) == 0); // our data is floats so channels will always be multiple of 4
const int kChunkBytes = 384;
const int kChunkSimdSize = kChunkBytes / 16;
static_assert((kChunkBytes % 16) == 0, "chunk bytes needs to be multiple of simd width");
uint8_t* dstPtr = dst;
int64_t ip = 0;
alignas(16) uint8_t prev[kMaxChannels] = {};
Bytes16 prev16 = SimdZero();
for (; ip < int64_t(dataElems) - (kChunkBytes - 1); ip += kChunkBytes)
{
// read chunk of bytes from each channel
Bytes16 chdata[kMaxChannels][kChunkSimdSize];
const uint8_t* srcPtr = src + ip;
// fetch data for groups of 4 channels, interleave
// so that first in chdata is (a0b0c0d0 a1b1c1d1 a2b2c2d2 a3b3c3d3) etc.
for (int ich = 0; ich < channels; ich += 4)
{
for (int item = 0; item < kChunkSimdSize; ++item)
{
Bytes16 d0 = SimdLoad(((const Bytes16*)(srcPtr)) + item);
Bytes16 d1 = SimdLoad(((const Bytes16*)(srcPtr + dataElems)) + item);
Bytes16 d2 = SimdLoad(((const Bytes16*)(srcPtr + dataElems * 2)) + item);
Bytes16 d3 = SimdLoad(((const Bytes16*)(srcPtr + dataElems * 3)) + item);
// interleaves like from https://fgiesen.wordpress.com/2013/08/29/simd-transposes-2/
Bytes16 e0 = SimdInterleaveL(d0, d2); Bytes16 e1 = SimdInterleaveR(d0, d2);
Bytes16 e2 = SimdInterleaveL(d1, d3); Bytes16 e3 = SimdInterleaveR(d1, d3);
Bytes16 f0 = SimdInterleaveL(e0, e2); Bytes16 f1 = SimdInterleaveR(e0, e2);
Bytes16 f2 = SimdInterleaveL(e1, e3); Bytes16 f3 = SimdInterleaveR(e1, e3);
chdata[ich + 0][item] = f0;
chdata[ich + 1][item] = f1;
chdata[ich + 2][item] = f2;
chdata[ich + 3][item] = f3;
}
srcPtr += 4 * dataElems;
}
if (channels == 16)
{
// channels == 16 case is much simpler
// read groups of data from stack, interleave, accumulate sum, store
for (int item = 0; item < kChunkSimdSize; ++item)
{
for (int chgrp = 0; chgrp < 4; ++chgrp)
{
Bytes16 a0 = chdata[chgrp][item];
Bytes16 a1 = chdata[chgrp + 4][item];
Bytes16 a2 = chdata[chgrp + 8][item];
Bytes16 a3 = chdata[chgrp + 12][item];
// now we want a 4x4 as-uint matrix transpose
Bytes16 b0 = SimdInterleave4L(a0, a2); Bytes16 b1 = SimdInterleave4R(a0, a2);
Bytes16 b2 = SimdInterleave4L(a1, a3); Bytes16 b3 = SimdInterleave4R(a1, a3);
Bytes16 c0 = SimdInterleave4L(b0, b2); Bytes16 c1 = SimdInterleave4R(b0, b2);
Bytes16 c2 = SimdInterleave4L(b1, b3); Bytes16 c3 = SimdInterleave4R(b1, b3);
// c0..c3 is what we should do accumulate sum on, and store
prev16 = SimdAdd(prev16, c0); SimdStore(dstPtr, prev16); dstPtr += 16;
prev16 = SimdAdd(prev16, c1); SimdStore(dstPtr, prev16); dstPtr += 16;
prev16 = SimdAdd(prev16, c2); SimdStore(dstPtr, prev16); dstPtr += 16;
prev16 = SimdAdd(prev16, c3); SimdStore(dstPtr, prev16); dstPtr += 16;
}
}
}
else
{
// general case: interleave data
uint8_t cur[kMaxChannels * kChunkBytes];
for (int ib = 0; ib < kChunkBytes; ++ib)
{
uint8_t* curPtr = cur + ib * kMaxChannels;
for (int ich = 0; ich < channels; ich += 4)
{
*(uint32_t*)curPtr = *(const uint32_t*)(((const uint8_t*)chdata) + ich * kChunkBytes + ib * 4);
curPtr += 4;
}
}
// accumulate sum and store
// the row address we want from "cur" is interleaved in a funky way due to 4-channels data fetch above.
for (int item = 0; item < kChunkSimdSize; ++item)
{
for (int chgrp = 0; chgrp < 4; ++chgrp)
{
uint8_t* curPtrStart = cur + (chgrp * kChunkSimdSize + item) * 4 * kMaxChannels;
for (int ib = 0; ib < 4; ++ib)
{
uint8_t* curPtr = curPtrStart;
// accumulate sum w/ SIMD
for (int ich = 0; ich < channels; ich += 16)
{
Bytes16 v = SimdAdd(SimdLoadA(&prev[ich]), SimdLoad(curPtr));
SimdStoreA(&prev[ich], v);
SimdStore(curPtr, v);
curPtr += 16;
}
// store
memcpy(dstPtr, curPtrStart, channels);
dstPtr += channels;
curPtrStart += kMaxChannels;
}
}
}
}
}
// any remainder
if (channels == 16)
{
for (; ip < int64_t(dataElems); ip++)
{
// read from each channel
alignas(16) uint8_t chdata[16];
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < 16; ++ich)
{
chdata[ich] = *srcPtr;
srcPtr += dataElems;
}
// accumulate sum and write into destination
prev16 = SimdAdd(prev16, SimdLoadA(chdata));
SimdStore(dstPtr, prev16);
dstPtr += 16;
}
}
else
{
for (; ip < int64_t(dataElems); ip++)
{
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t v = *srcPtr + prev[ich];
prev[ich] = v;
*dstPtr = v;
srcPtr += dataElems;
dstPtr += 1;
}
}
}
}
I told you it is getting long! Did it help? “K” case: decompression unfilter WinVS 15ms, WinClang 15ms, Mac 16ms (“H” was 18, 14, 24)
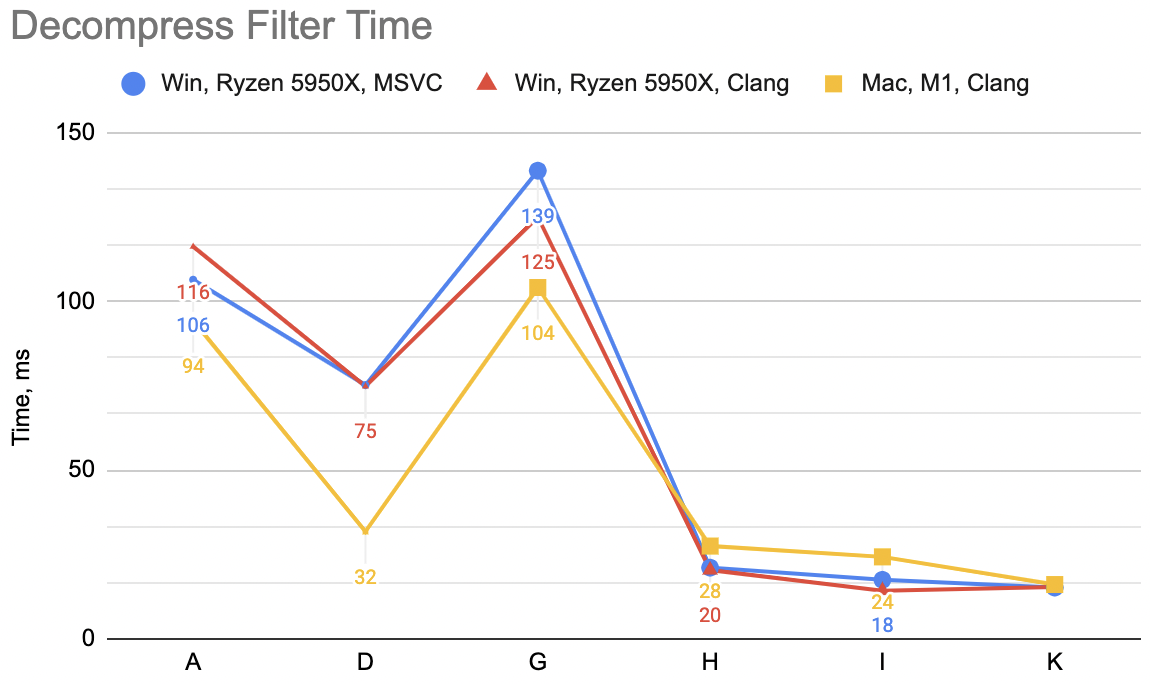
Ok, it does significantly help Mac (Apple M1/NEON) case; helps a bit on Windows PC too.
Conclusions
All in all, for the decompression unfilter we went from super simple code in part 3 (“A”) to a naïve attempt at SIMD (“D”) to this fairly involved “K” variant, and their respective timings are:
- Ryzen 5950X, Windows, VS2022: 106→75→15ms. Clang 15: 116→75→15ms.
- Apple M1, Clang 14: 94→32→16ms.
The performance is 5-8 times faster, which is nice. Note: it’s entirely possible that I have misunderstood Fabian’s advice, and/or did it wrong, or just left some other speedup opportunities lying on the floor.
The filtering part is faster now, great. How does this affect the overall process, when we put it next to the actual data compression & decompression? After all, this is what we are really interested in.
Here they are (click for interactive chart; solid thick line: this post, solid thin line: “D” from previous post). Windows MSVC, Windows Clang, Mac Clang:
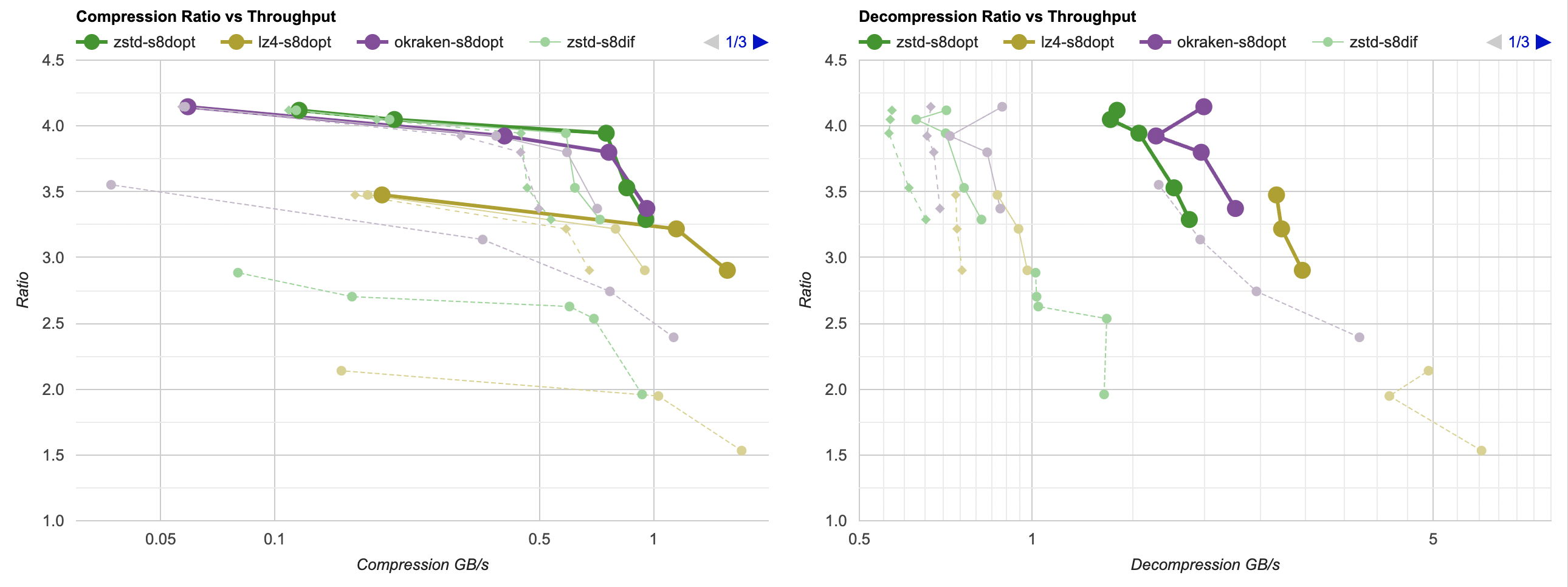
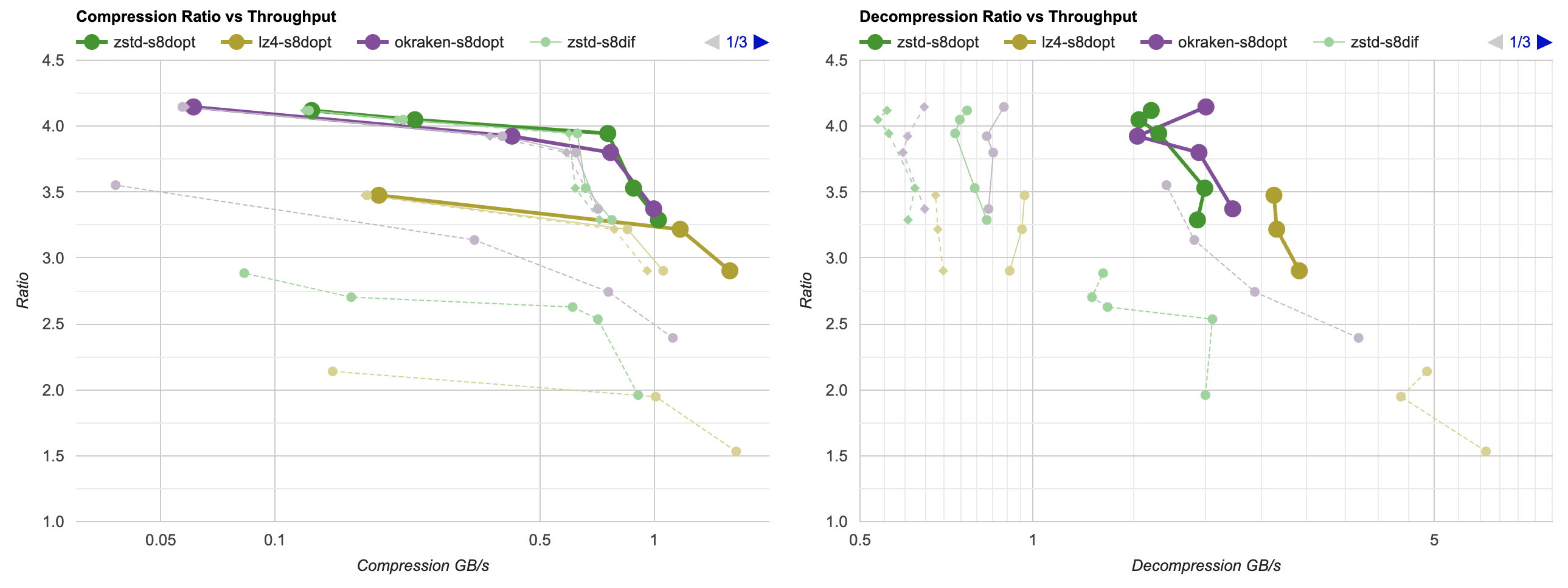
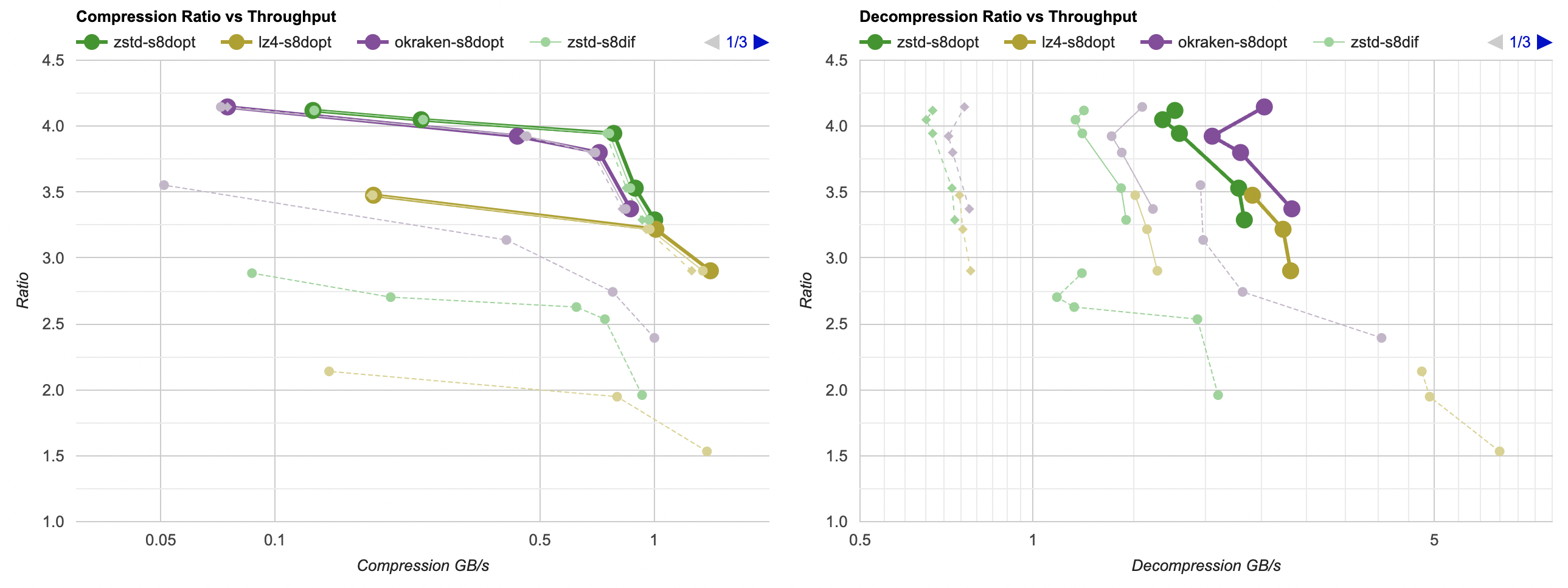
Hey look! If you are using zstd, both compression and decompression is faster and better ratio with the data filtering applied. For LZ4 the decompression does not quite reach the 5GB/s that it can do without data filtering, but it does go up to 2.5GB/s which is way faster than 0.7GB/s that it was going on in the “A” approach. And the compression ratio is way better than just LZ4 can achieve.
The code is quite a bit more complex though. Is all that code complexity worth it? Depends.
- The code is much harder to follow and understand.
- However, the functionality is trivial to test, and to ensure it keeps on working via tests.
- This is not one of those “oh but we need to keep it simple if it needs to get changed later” cases. You either do “combine streams, decode delta”, or you do something else. Once or if you settled onto that data format, the code to achieve that un-filtering step needs to do exactly just that. If you need to do something else, throw away this code and write code to do that other thing!
- If “data un-filtering” (transpose, decode delta) is critical part of your library or product, or just a performance critical area, then it might be very well worth it.
Nothing in the above is “new” or noteworthy, really. The task of “how to filter structured data” or “how to transpose data fast” has been studied and solved quite extensively. But, it was a nice learning experience for me!
What’s next
I keep on saying that I’d look into lossy compression options, but now many (read: more than one!) people have asked “what about Blosc?” and while I was aware of it for a number of years, I have never actually tested it. So I’m gonna do that next!