Unity has a problem

From the outside, Unity lately seems to have a problem or two. By “lately”, I mean during the last decade, and by “a problem or two”, I mean probably over nine thousand problems. Fun! But what are they, how serious they are, and what can be done about it?

Unity is a “little engine that could”, that started out in the year 2004. Almost everything about games and related industries was different compared to today (Steam did not exist for 3rd party games! The iPhone was not invented yet! Neural networks were an interesting but mostly failed tinkering area for some nerds! A “serious” game engine could easily be like “a million dollars per project” in licensing costs! …and so on). I joined in early 2006 and left in early 2022, and saw quite an amazing journey within – against all odds, somehow, Unity turned from the game engine no one has heard about into arguably the most popular game engine.

But it is rare for something to become popular and stay popular. Some of that is a natural “cycle of change” that happens everywhere, some of that is external factors that are affecting the course of a product, some is self-inflicted missteps. For some other types of products or technologies, once they become an “industry standard”, they kinda just stay there, even without seemingly large innovations or a particular love from the user base – they have become so entrenched and captured so much of the industry that it’s hard to imagine anything else. Photoshops and Offices of the world come to mind, but even those are not guaranteed to forever stay the leaders.

Anyway! Here’s a bunch of thoughts on Unity as I see them (this is only my opinion that is probably wrong, yadda yadda).

Caveat: personally, I have benefitted immensely from Unity going public. It did break my heart and make my soul hollow, but financially? Hoo boy, I can’t complain at all. So everything written around here should be taken with a grain of salt, this is a rich, white, bald, middle aged man talking nonsense.

You don’t get rocket fuel to go grocery shopping

For better or worse, Unity did take venture capital investment back in 2009. The company and the product was steadily but slowly growing before that. But it also felt tiny and perhaps “not quite safe” – I don’t remember the specifics, but it might have very well been that it was always just “one unlucky month” away from running out of money. Or it could have been wiped out by any of the big giants at the time, with not much more than an accidental fart in our direction from their side. Microsoft coming up with XNA, Adobe starting to add 3D features to Flash, Google making O3D browser plugin technology – all of those felt like possible extinction level events. But miraculously, they were not!

I don’t even remember why and who decided that Unity should pursue venture capital. Might have happened in one of those “bosses calls” that were about overall strategy and direction that I was a part of, until I wasn’t but everyone forgot to tell me. I just kept on wondering why we stopped them… turns out we did not! But that’s a story for another day :)

The first Series A that Unity raised in 2009 ($5.5M), at least to me, felt like it removed the constant worry of possibly not making it to the next month.

However. VC money is like rocket fuel, and you don’t get rocket fuel just to continue grocery shopping every day. You have to get to space.

Many clever people have written a lot about whether the venture capital is a good or a bad model, and I won’t repeat any of that here. It does allow you to go to space, figuratively; but it also only allows you to go to space. Even if you’d rather keep on going to the grocery store forever.

A bunch of old-time Unity users (and possibly employees) who reminisce about “oh, Unity used to be different Back In The Day” have these fond memories of the left side of the graph below. Basically, before the primary goal of the company became “growth, growth and oh did I mention growth?”.

Here’s Unity funding rounds (in millions of $ per year), and Unity acquisitions (in number per year) over time. It might be off or incomplete (I just gathered data from what’s on the internet, press releases and public financial reports), but overall I think it paints an approximately correct picture. Unity had an IPO in 2020 ($1.3B raised as part of that), and in 2021 raised an additional $1.5B via convertible notes. Also went on a large acquisition spree in 2019-2021.

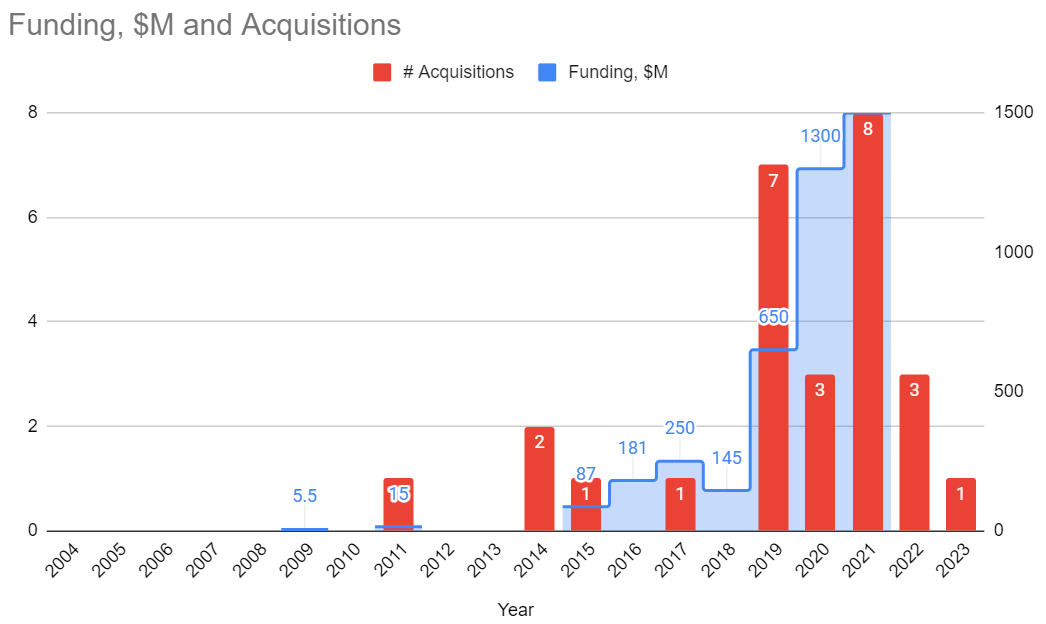
The “good old Unity” times that some of you fondly remember, i.e. Unity 4.x-5.x era? That’s 2012-2015. Several years after the initial Series A, but well before the really large funding rounds and acquisitions of 2019+. The “raising money is essentially free” situation that was a whole decade before 2020 probably fueled a lot of that spending in pursuit of “growth”.

Vision and Growth

In some ways, being a scrappy underdog is easy – you do have an idea, and you try to make that a reality. There’s a lot of work, a lot of challenges, a lot of unexpected things coming at you, but you do have that one idea that you are working towards.

On June 2005 the Unity website had this text describing what all of this is about:

“We create quality technology that allows ourselves and others to be creative in the field of game development. And we create games to build the insight necessary to create truly useful technology.

We want our technology to be used by creative individuals and groups everywhere to experiment, learn, and create novel interactive content.

We’re dedicated to providing a coherent and clear user experience. What makes us great is our constant focus on the clear interplay of features and functionality from your perspective.”

Whereas in 2008, the “about” page was this:

For comparison, right now in 2024 the tagline on the website is this: “We are the world’s leading platform for creating and operating interactive, real-time 3D (RT3D) content. We empower creators. Across industries and around the world.” Not bad, but also… it does not mean anything.

And while you do have this vision, and are trying to make it a reality, besides the business and lots-of-work struggles, things are quite easy. Just follow the vision!

But then, what do you do when said vision becomes reality? To me, it felt like around year 2012 the vision of “Unity is a flexible engine targeted at small or maybe medium sized teams, to make games on many platforms” was already true. Mobile gaming market was still somewhat friendly to independent developers, and almost everyone there was using Unity.

And then Unity faced a mid-life crisis. “Now what? Is this it?”

From a business standpoint, and the fact that there are VCs who would eventually want a return on their investment, it is not enough to be merely an engine that powers many games done by small studios. So multiple new directions emerged, some from a business perspective, some from “engine technology” perspective. In no particular order:

There are way more consumers than there are game developers. Can that somehow be used? Unity Ads (and several other internal initiatives, most of which failed) is a go at that. I have no idea whether Unity Ads is a good or bad network, or how it compares with others. But it is a large business branch that potentially scales with the number of game players.

There was a thought that gathering data in the form of analytics would somehow be usable or monetizable. “We know how a billion people behave across games!” etc. Most of that thought was before people, platforms and laws became more serious about privacy, data gathering and user tracking.

Other markets besides gaming. There are obvious ones that might need interactive 3D in some way: architecture, construction, product visualization, automotive, medical, movies, and yes, military. To be fair, even without doing anything special, many of those were already using Unity on their own. But from a business standpoint, there’s a thought “can we get more money from them?” which is entirely logical. Some of these industries are used to licensing really shoddy software for millions of dollars, afterall.

Within gaming, chasing “high end” / AAA is very alluring, and something that Unity has been trying to do since 2015 or so. Unity has been this “little engine”, kinda looked down on by others. It was hard to hire “famous developers” to work on it. A lot of that changed with JR becoming the CEO. Spending on R&D increased by a lot, many known and experienced games industry professionals were convinced to join, and I guess the compensation and/or prospect of rising stock value was good enough too. Suddenly it felt like everyone was joining Unity (well, the ones who were not joining Epic or Oculus/Facebook at the time).

Things were very exciting!

Except, growth is always hard. And growing too fast is dangerous.

What is our vision, again?

Unity today is way more capable engine technology wise, compared to Unity a decade ago. The push for “high end” did deliver way improved graphics capabilities (HDRP), artist tooling (VFX graph, shader graph, Timeline etc.), performance (DOTS, Burst, job system, internal engine optimizations), and so on.

But also, somehow, the product became much more fractured, more complex and in some ways less pleasant to use.

Somewhat due to business reasons, Unity tried to do everything. Mobile 2D games? Yes! High end AAA console games? Yes (pinky promise)! Web games? Sure! People with no experience whatsoever using the product? Of course! Seasoned industry veterans? Welcome! Small teams? Yes! Large teams? Yes!

At some point (IIRC around 2017-2018) some of the internal thinking became “nothing matters unless it is DOTS (high-end attempt) or AR (for some reason)”. That was coupled with, again, for some reason, “all new code should be written in C#” and “all new things should be in packages”. These two led to drastic slowdowns in iteration time – suddenly there’s way more C# code that has to be re-loaded every time you do any C# script change, and suddenly there’s way more complex compatibility matrix between which packages work with what.

The growth of R&D led to vastly different styles and thinking about the product, architecture and approaches of problem solving. Random examples:

• Many AAA games veterans are great at building AAA games, but not necessarily great at building a platform. To them, technology is used by one or, at most, a handful of productions. Building something that is used by millions of people and tens of thousands of projects at once is a whole new world.
• There was a large faction coming from the web development world, and they wanted to put a ton of “web-like” technologies into the engine. Maybe make various tools work in the browser as well. Someone was suggesting rewriting everything in JavaScript, as a way to fix development velocity, and my fear is that they were not joking.
• A group of brilliant, top-talent engineers seemed to want to build technology that is the opposite of what Unity is or has been. In their ideal world, everyone would be writing all the code in SIMD assembly and lockless algorithms.
• There was a faction of Unity old-timers going “What are all these new ideas? Why are we doing them?”. Sometimes raising good questions, sometimes resisting change just because. Yes, I’ve been both :)

All in all, to me it felt like after Unity has arguably achieved “we are the engine of choice for almost every small game developer, due to ease of use, flexibility and platform reach”, the question on what to do next coupled with business aspects made the engine go into all directions at once. Unity stopped having, err, “unity” with itself.

Yes, the original DOTS idea had a very strong vision and direction. I don’t know what the current DOTS vision is. But to me the original DOTS vision felt a lot like it is trying to be something else than Unity – it viewed runtime performance as the most important thing, and assumed that everyone’s main goal is getting best possible performance, thinking about data layout, efficient use of CPU cores and so on. All of these are lovely things, and it would be great if everyone thought of that, sure! But the amount of people who actually do that is like… all seventy of them? (insert “dozens of us!” meme)

What should Unity engine vision be?

That’s a great question. It is easier to point out things that are wrong, than to state what would be the right things. Even harder is to come up with an actionable plan on how to get from the current non-ideal state to where the “right things” are.

So! Because it is not my job to make hard decisions like that, I’m not going to do it :) What I’ll ponder about, is “what Unity should / could be, if there were no restrictions”. A way easier problem!

In my mind, what “made Unity be Unity” originally, was a combination of several things:

• Ease of prototyping: the engine and tooling is flexible and general enough, not tied into any specific game type or genre. Trying out “anything” is easy, and almost anything can be changed to work however you want. There’s very few restrictions; things and features are “malleable”.
• Platforms: you can create and deploy to pretty much any relevant platform that exists.
• Extensible: the editor itself is extremely extensible - you can create menus, whole new windows, scene tooling, or whatever workflow additions are needed for your project.
• Iteration time and language: C# is a “real” programming language with an enormous ecosystem (IDEs, debuggers, profilers, libraries, knowledge). Editor has reloading of script code, assets, shaders, etc.

I think of those items above as the “key” to what Unity is. Notice that for example “suitable for giant projects” or “best performance in the world” are not on the list. Would it be great to have them? Of course, absolutely! But for example it felt like the whole DOTS push was with the goal of achieving best runtime performance at the expense of the items above, which creates a conflict.

In the early days of Unity, it did not even have many features or tooling built-in. But because it is very extensible, there grew a whole ecosystem with other people providing various tools and extensions. Originally we thought that Asset Store would be mostly for, well, “assets” - models and sounds and texture packs. Sure it has that, but by far the most important things on the asset store turned out to be various editor extensions.

This is a double-edged sword. Yes it did create an impression, especially compared to say Unreal, that “Unity has so few tools, sure you can get many on the asset store but they should be built-in”. In the early days, Unity was simply not large enough to do everything. But with the whole push towards high-end and AAA and “more artist tooling”, it did gain more and more tools built-in (timeline, shader graph, etc.). However, with varying degrees of success.

Many of the new features and workflows added by Unity are (or at least feel like) they are way less “extensible”. Sure, here’s a feature, and that’s it. Can you modify it somehow or bend to your own needs in an easy way? Haha lol, nope. You can maybe fork the whole package, modify the source code and maintain your fork forever.

What took me a long time to realize, is that there is a difference between “extensible” and “modifiable”.The former tries to add various ways to customize and alter some behavior. The latter is more like “here’s the source code, you can fork it”. Both are useful, but in very different scenarios. And the number of people who would want to fork and maintain any piece of code is very small.

So what would my vision for Unity be?

Note that none of this are original ideas, discussions along this direction (and all the other possible directions!) have been circulated inside Unity forever. Which direction(s) will actually get done is anyone’s guess though.

I’d try to stick to the “key things” from the previous section: malleability, extensibility, platforms, iteration time. Somehow nail those, and never lose sight of them. Whatever is done, has to never sacrifice the key things, and ideally improve on them as well.

Make the tooling pleasant to use. Automate everything that is possible, reduce visible complexity (haha, easy, right?), in general put almost all effort into “tooling”. Runtime performance should not be stupidly bad, somehow, but is not the focus.

Achieving the above points would mean that you have to nail down:

• Asset import and game build pipeline has to be fast, efficient and stable.
• Iteration on code, shaders, assets has to be quick and robust.
• Editor has to have plenty of ways to extend itself, and lots of helper ways to build tools (gizmos, debug drawing, tool UI widgets/layouts/interaction). For example, almost everything that comes with Odin Inspector should be part of Unity.
• In general everything has to be flexible, with as few limitations as possible.

Unity today could be drastically improved in all the points above. Editor extensibility is still very good, even if it is made confusing with presence of multiple UI frameworks (IMGUI, which almsot everything is built on, and UIToolkit, which is new).

To this day I frankly don’t understand why Unity made UIToolkit, and also why it took so many resources (in terms of headcount and development time). I’d much rather liked Unity to invest in IMGUI along the lines of PanGui.

Additionally, I’d try to provide layered APIs to build things onto. Like a “low level, for experts, possibly Unity people themselves too” layer, and then higher level, easier to use, “for the rest of us” that is built on top of the low level one. Graphics is used to be my area of expertise, so for the low level layer you would imagine things like data buffers, texture buffers, ability to modify those, ability to launch things on the GPU (be it draw commands or compute shader dispatches, etc.), synchronization, etc. High level layer would be APIs for familiar concepts like “a mesh” or “a texture” or “a material”.

The current situation with Unity’s SRPs (“scriptable render pipelines” - URP and HDRP being the two built-in ones) is, shall we say, “less than ideal”. From what I remember, the original idea behind making the rendering engine be “scriptable” was something different than what it turned out to be. The whole SRP concept started out at a bit unfortunate time when Burst and C# Job System did not exist yet, the whole API perhaps should have been a bit different if these two were taken to heart. So today SRP APIs are in a weird spot of being neither low level enough to be very flexible and performant, nor high level enough to be expressive and easy to use.

In my mind, any sort of rendering pipeline (be it one of default ones, or user-made / custom) would work on the same source data, only extending the data with additional concepts or settings when absolutely needed. For example, in the old Unity’s built-in render pipeline, you had a choice between say “deferred lighting” and “per-vertex lighting”, and while these two target extremely different hardware capabilities, result in different rendering and support different graphics features, they work on the same data. Which means the choice between them is “just a setting” somewhere, and not an up-front decision that you have to make before even starting your project. Blender’s “render engines” are similar here - the “somewhat realtime” EEVEE and “offline path tracer” Cycles have different tradeoffs and differ in some features, but they both interpret the same Blender scene.

Within Unity’s SRP land, what started out initially as experiments and prototypes to validate the API itself – “is this API usable to build a high end PBR renderer?” and “is this API usable to build a minimalistic and lean low-end renderer?”, ended up shipping as a very in-your-face user setting. They should have been prototypes, and then the people making the two should have gathered together, decide on the learnings and findings about the API, and think about what to do for reals. But reality happened, and now there are two largely incompatible render pipelines. Oh well!

Oh, one more additional thing, just make source code available ffs. There’s nothing you are gaining by making people jump through licensing, legal and cost hoops to get to it, and you’re losing a lot. Being able to read, reason and debug source code, and maybe make a hotfix or two are very important to finish any complex project.

Ok, but who that engine would be for? That’s a complex question, but hey it is not my job to figure out the answers. “A nice easy to use game engine for prototypes and small teams”, I think, would definitely not be an IPO material, and probably not VC material either. Maybe it could be a healthy and sustainable business for a 50 employee sized company. Definitely not something that grew big, then stalled, then <who knows what will happen next> but it made a few dozen people filthy rich :)

Wot about AI?

I know next to nothing about all the modern AI (GenAI, LLMs etc.) thingies. It is a good question, whether the “current way” of building engines and tools is a good model for the future.

Maybe all the complex setups and lighting math that they do within computer graphics is kinda pointless, and you should just let a giant series of matrix multiplications hallucinate the rendered result? It used to be a joke that “the ideal game tool is a text field and a Make Game button”, but that joke is no longer funny now.

Anyhoo, given that I’m not an expert, I don’t have an opinion on all of this. “I don’t know!”

But what I do occasionally think about, is whether Unity is in a weird place of not being low-level enough, and not high-level enough at the same time.

A practical example would be, that within Unity there does not exist a concept like “this surface is made of pine tree” – to make a “wooden” thing in Unity, you have to get some wood textures, create a Material, pick a Shader, and set up parameters on that. The surface has to be a Mesh, and the object have Mesh Renderer and a (why?) Mesh Filter. Then you need to have a Collider, and set up some sort of logic of “play this sound when something hits it”, and the sounds have to be made by someone. The pine surface needs to have a Physics Material on it, with, uhh, some sort of friction, restitution and bounciness coefficients? Oh, if it moves it should have a Rigidbody with a bunch of settings. Should the surface break when something hits it hard enough? Where to even start on that?

Is it great that Unity allows you to specify all of these settings in minute detail? For some cases, yes maybe. I would imagine that many folks would happily take a choice of “make this look, feel and behave as if it is made of pine wood” however. So maybe the layer of Unity that people mostly interact with should be higher level than that of Box Colliders and Rigidbodies and Mesh Renderers. I don’t have an answer on how that level should look like exactly, but it is something to ponder about.

At the same time, the low-levels of Unity are not low-level enough. Looking at graphics related APIs specifically, a good low-level API would expose things like mesh shaders, and freely threaded buffer creation, and bindless resources by now.

Where I lose my train of thought and finish this post

Anyway. I was not sure where I was going with all of the above, so let’s say it is enough for now. I really hope that Unity decides where it actually wants to go, and then goes there with a clear plan. It has been sad to watch many good people leave or be laid off, many companies that made great Unity games switch away from Unity. The technology and the good people within the company deserve so much better than a slow moving trainwreck.

I did a bunch of work for Blender 4.1 video sequence editor, and since no one revoked my commit access, I continued in the same area for Blender 4.2. Are you one of the approximately seven Blender VSE users? Read on then!

Blender 4.2 has just shipped, and everything related to Video Sequence Editor is listed on this page. Probably half of that is my fault work, and since 4.2 is a long term support (LTS) release, this means I’ll have to fix any bugs or issues about that for three more years, yay :)

Visual updates, and rendering strip widgets in a shader

What started out as a casual “hey could we have rounded corners?” question in some chat or a design task, snowballed into, well, rounded corners. Corner rounding for UI controls and widgets is so ubiquitous these days, that it feels like it is a trivial thing to do. And it would… if you had a full vector graphics renderer with anti-aliased clipping/masking lying around. But I do not.

The VSE timeline “widgets” in Blender 4.1 and earlier are pretty much just “rectangles and lines”. The “widget control” is surprisingly complex and can have many parts in there – besides the obvious ones like image thumbnail, audio waveform or title text, there’s background, color tag overlay, animation curve (volume or transition) overlay, fade transition triangle, retiming keys, transformation handles, meta strip content rectangles, “locked” diagonal stripes and some others. Here’s a test timeline showing most of the possible options, in Blender 4.1:

Thumbnails, waveforms, curves, locked stripes and texts are drawn in their own ways, but everything else is pretty much just a bunch of “blend a semitransparent rectangle” or “blend a semitransparent line”.

How do you make “rounded corners” then? Well, “a rectangle” would need to gain rounded corners in some way. You could do that by replacing rectangle (two triangles) with a more complex geometry shape, but then you also want the rounded corners to be nicely anti-aliased. What is more complicated, is that you want “everything else” to get rounded too (e.g. strip outline or border), or masked by the rounded corner (e.g. diagonal stripes to indicate “locked” state, or the image thumbnail should not “leak” outside of the rounded shape).

Another way to do all of this, ever since Inigo Quilez popularized Signed Distance Fields, would be to draw each widget as a simple rectangle, and do all the “rounded corners” evaluation, masking and anti-aliasing inside a shader. I wanted to play around with moving all (or most) of strip “widget” into a dedicated shader for a while, and so this was an excuse to do exactly that. The process looked like this:

1. Stall and procrastinate for a month, thinking how scary it will be to untangle all the current VSE widget drawing code and move that into a shader, somehow. I kept on postponing or finding excuses to not do it for a long time.
2. Actually try to do it, and turns out that was only a day of work (#122576). Easy!
3. Spend the next month making a dozen more pull requests (#122764, #122890, #123013, #123065, #123119, #123221, #123369, #123391, #123431, #123515, #124210, #124965, #125220), making the rounded corners actually work. Some of these were fixes (snapping to pixel grid, DPI awareness, precision issues), some were design and visual look tweaks.

All of that, together with various other design and strip handle UX updates done by Richard Antalik and Pablo Vazquez, resulted in Blender 4.2 VSE looking like this now:

I’ve also implemented visual indication of missing media (strips that point to non-existing image/movie/sound files) #116869; it can be seen in the screenshot above too.

Text shadows & outlines

Text strips in VSE had an option for a drop-shadow, but it was always at fixed distance and angle from the text, making it not very useful in general case. I made the distance and angle configurable, as well as added shadow blur option. While at it, text also got an outline option (#121478).

Outlines are implemented with Jump-Flooding algorithm, as wonderfully described by Ben Golus in “The Quest for Very Wide Outlines” blog post.

Performance

While Blender 4.1 brought many and large performance improvements to VSE, the 4.2 release is not so big. There is some performance work however:

“Occlusion culling” for opaque images/movies (#118396). VSE already had an optimization where a strip that is known to be fully opaque and covers the whole screen, stops processing of all strips below it (since they would not be visible anyway). Now the same optimization happens for some cases of strips that do not cover the whole screen: when a fully opaque strip completely covers some strip that is under it, the lower strip is not evaluated/rendered.

The typical case is letterboxed content: there’s black background that covers the whole screen, but then the actual “content” only covers a smaller area. On Gold previs, this saved about 7% of total render time. Not much, but still something.

Optimize parts of ffmpeg movie decoding

• Cache ffmpeg libswscale color conversion contexts (#118130). Before this change, each individual movie strip would create a “color conversion context” object, that is mostly used to do YUV↔RGB conversion. However, most of them end up being exactly the same, so have a pool of them and reuse them as needed.
• Stop doing some redundant work when starting movie strip playback (#118503). Not only this made things faster, but also removed about 200 lines of code. Win-win!
• (not performance per se, but eh) Remove non-ffmpeg AVI support (#118409). Blender had very limited .avi video support that does not go through ffmpeg. Usefulness of that was highly questionable, and mostly a historical artifact. Poof, now it is gone, along with 3600 lines of code. 🎉

What’s Next

I investigated support for 10/12 bpp and HDR videos, but did not get anything finished in time for Blender 4.2. It does not help that I know nothing about video codecs or color science lol :) But maybe I should continue on that.

The VSE timeline drawing has obvious “would be nice to finish” parts, some of which would address performance issues too. Right now most of strip control is drawn inside a dedicated GPU shader, but there are bits that are still drawn separately (thumbnails, audio waveforms, meta strip contents, animation curve overlays). Getting them to be drawn inside the same shader would (or could?) make CPU side work much simpler.

VSE feature within Blender overall could benefit from a thousand small improvements, but also perhaps the relevant people should discuss what is the bigger picture and actual plans for it. It is good to continue doing random incremental improvements, but once in a while discussing and deciding “where exactly we want to end up at?” is also useful. Maybe we should do that soon.

That’s it!

Just spent 10 days around in Kyrgyzstan, so here’s a bunch of pictures!

Overall this was a “botanical trip”. There’s a local group of gardeners and related people, who do journeys through various famous and beautiful gardens, and so on. This year, they decided to not go through literal gardens, but rather visit foots and valleys of Tian Shan, where a lot of decorative plants originate from and/or just grow in the wilderness. Now, I know next to nothing about plants, flowers or gardening, but my wife does, and I just tagged along.

Did you know? Tulips originate from Tian Shan. Another factoid: Yersinia Pestis bacterium that caused Black Death also probably originates from Tian Shan.

So! Our itinerary was like, visit valleys near the mountains, as well as whatever “must see” items within Kyrgyzstan are. We did not go into the actual mountains for several reasons, 1) high up there’s no vegetation anymore! and 2) this was an easy trip for non-professionals.

The nature there is absolutely beautiful! I mean, look at it:

It never felt crowded or “too touristy”; majority of tourists we met were people taking cross-Central Asia trips on motorcycles. Lack of convenient infrastucture (many places only have gravel roads towards them) and lack of “I can converse in English” options probably keep many tourists away (language to get by is Russian).

In towns and cities, I did not expect to see so many Soviet-era relics. Here (in Lithuania) most of them got wiped away or relegated to museums, but in Kyrgyzstan there are sculptures of Lenin everywhere, Soviet-time coats of arms on government buildings, etc. “Interesting”!

What follows is a bag of photos roughly grouped by geographical area.

Ala-Archa Nature Park

Bishkek

Burana Tower

Konorchek Canyon

Now… we did not get to the actual canyon, since en route my wife dislocated her kneecap :( We did get to try out how ambulances and hospitals work (on Sunday! 40km away from the hospital!). Everyone was very nice and total cost was around €10 (ambulance & personell: free, xray: €3, materials for the cast: €7). For the rest of the trip the leg was in a plaster cast though.

Issyk-Kul

Skazka Canyon

Barskoon Waterfalls

Towards Song-Köl

Song-Köl

Moldo-Ashuu Pass

Tash Rabat Caravanserai

I collected all the dogs

Lots of German Shepherds around, that actually do shepherding (of lambs, cows, horses and yaks), an occasional Taigan, and a bunch of other random dogs.

Carpets! They are important

Misc

And that’s it!

You know Playdate, the cute yellow console with a crank? I think I saw it in person last year via Inês, and early this year they started to have Lithuania as a shipping destination, so I got one. And then what would I do with it? Of course, try to make a demoscene demo :)

First impressions

The device is cute. The SDK is simple and no-nonsense (see docs). I only used the C part of SDK (there’s also Lua, which I did not use). You install it, as well as the official gcc based toolchain from ARM, and there you go. SDK provides simple things like “here’s the bitmap for the screen” or “here’s which buttons are pressed” and so on.

The hardware underneath feels similar to “about the first Pentiums” era - single core CPU at 180MHz (ARM Cortex-M7F), with hardware floating point (but no VFP/NEON), 16MB RAM, there’s no GPU. Screen is 400x240 pixels, 1 bit/pixel – kinda Kindle e-ink like, except it refreshes way faster (can go up to 50 FPS). Underlying operating system seems to be FreeRTOS but nothing about it is exposed directly; you just get what the SDK provides.

At first I tried checking out how many polygons can the device rasterize while keeping 30 FPS:

But in the end, going along with wise words of kewlers and mfx, the demo chose to use zero polys (and… zero shaders).

Packaging up the “final executable” of the demo felt like a breath of fresh air. You just… zip up the folder. That’s it. And then anyone with a device can sideload it from anywhere. At first I could not believe that it would actually work, without some sort of dark magic ritual that keeps on changing every two months. Very nice.

By the way, check out the “The Playdate Story: What Was it Like to Make Handheld Video Game System Hardware?” talk by Cabel Sasser from GDC 2024. It is most excellent.

The demo

I wanted to code some oldskool demo effects that I never did back when 30 years ago everyone else was doing them. You know: plasma, kefren bars, blobs, starfield, etc.

Also wanted to check out how much of shadertoy-like raymarching could a Playdate do. Turns out, “not a lot”, lol.

And so the demo is just that: a collection of random scenes with some “effects”. Music is an old GarageBand experiment that my kid did some years ago.

• Video: device playing it (youtube / mp4 file), just the screen (youtube / mp4 file)
• Playdate build: Nesnausk_CrankTheWorld.pdx.zip (3MB), should also work in Playdate Simulator on Windows.
• pouët: https://www.pouet.net/prod.php?which=96955
• Source code: https://github.com/aras-p/demo-pd-cranktheworld
• Took 4th place at Outline 2024 “Newskool Demo” category.
• Credits: everything except music – NeARAZ, music – stalas001.

Tech bits

Playdate uses 1 bit/pixel screen, so to represent “shades of gray” for 3D effects I went the simple way and just used a static screen-size blue noise texture (from here). So “the code” produces a screen-sized “grayscale” image with one byte per pixel, and then it is dithered through the blue noise texture into the device screen bitmap. It works way better than I thought it would!

All the raymarched/raytraced scenes are way too slow to calculate each pixel every frame (too slow with my code, that is). So instead, calculate only every Nth pixel each frame, with update pattern similar to ordered dithering tables.

• Raytraced spheres: update 1 out of 6 pixels every frame (in 3x2 pattern),
• Raymarched tunnel/sponge/field: update 1 out of 4 pixels every frame (in 2x2 pattern), and run everything at 2x2 lower resolution too, “upscaling” the rendered grayscale image before dithering. So effectively, raymarching 1/16th the amount of screen pixels each frame.
• Other simpler scenes: update 1 out of 4 pixels every frame.

You say “cheating”, I say “free motion blur” or “look, this is a spatial and temporal filter just like DLSS, right?” :)

For the raymarched parts, I tried to make them “look like something” while keeping the number of march iterations very limited, and doing other cheats like using too large ray step size which leads to artifacts but hey no one knows what is it supposed to look like anyway.

All in all, most of the demo runs at 30 FPS, with some parts dropping to about 24 FPS.

Size breakdown: demo is 3.1MB in size, out of which 3MB is the music track :) And that is because it is just an ADPCM WAV file. The CPU cost of doing something like MP3 playback was too high, and I did not go the MIDI/MOD/XM route since the music track comes from GarageBand.

Some of the scenes/effects are ripped off inspired by other shadertoys or demos:

• twisty cuby by DJDoomz
• Ring Twister by Flyguy
• Pretty Hip by Fabrice Neyret
• Xor Towers by Greg Rostami
• Menger Sponge Variation by Shane
• Puls by Řrřola

When the music finishes, the demo switches to “interactive mode” where you can switch between the effects/scenes with Playdate A/B buttons. You can also use the crank to orbit/rotate the camera or change some other scene parameter. Actually, you can use the crank to control the camera during the regular demo playback as well.

All in all, this was quite a lot of fun! Maybe I should make another demo sometime.

Two months ago I started to contribute a bit of code to Blender’s Video Sequence Editor (VSE). Did you know that Blender has a suite of video editing tools? Yeah, me neither :) Even the feature page for it on the website looks… a bit empty lol.

Do I know anything at all about video editing, timelines, sequencers, color grading, ffmpeg, audio mixing and so on? Of course not! So naturally, that means I should start to tinker with it.

Wait what?

How does one accidentally start working on VSE?

You do that because you decide to check out Unity’s Unite 2023 conference in Amsterdam, and to visit some friends. For a spare half-a-day after the conference, you decide to check out Blender HQ. There, Francesco and Sergey, for some reason, ask you whether you’d like to contribute to VSE, and against your better judgement, you say “maybe?”.

So that’s how. And then it feels pretty much like this:

I started to tinker with it, mostly trying to do random “easy” things. By easy, I mean performance optimizations. Since, unless the code complexicates a lot, they are hard to argue against. “Here, this thing is 2x faster now”, in most places everyone will react with “oh nice!”. Hopefully.

So, two months of kinda-partime tinkering in this area that I did not even know existed before, and Blender VSE got a small set of improvements for upcoming Blender 4.1 (which just became beta and can be downloaded from usual daily builds). Here they are:

Snappier Timeline drawing

VSE timeline is the bottom part of the image above. Here it is zoomed out into the complete Sprite Fright edit project, with about 3000 “strips” visible at once. Just scrolling and panning around in that timeline was updating the user interface at ~15 frames per second.

Now that’s 60+ frames per second (#115311). Turns out, submitting graphics API draw calls two triangles at a time is not the fastest approach, heh. Here’s that process visualized inside the most excellent Superluminal profiler – pretty much all the time is spent inside “begin drawing one quad” and “finish drawing one quad” functions 🤦

As part of that, audio waveforms display also got some weirdness about it fixed, some UI polish tweaks, and now is on by default (#115274).

Scopes

VSE has options to display typical “scopes” you might expect: image histogram, waveform, vectorscope. Here’s their look, “before” on the left side, “now” on the right.

Histogram was drawn as pixelated image, with very saturated colors. Draw as nicer polygons, with a grid, and less saturation (#116798):

Waveform (here shown in “parade” option) was saturating very quickly. Oh, and make it 15x faster with some multi-threading (#115579).

Vectorscope’s outer color hexagon looked very 90s with all the pixelation. Copy the updated image editor vectorscope design, and voilà (#117738):

While at it, the “show overexposed regions” (“zebra stripes”) option was also sped up 2x-3x (#115622).

All these scopes (and image editor scopes) should at some point be done on the GPU with compute shaders, of course. Someday.

ffmpeg bits

Blender primarily uses ffmpeg libraries for audio/video reading and writing. That suite is famous for the extremely flexible and somewhat intimidating command line tooling, but within Blender the actual code libraries like libavcodec are used. Among other things, libswscale is used to do movie frame RGB↔YUV conversion. Turns out, libswscale can do those parts multi-threaded for a while by now, it’s just not exactly intuitive how to achieve that.

Previous code was like:

// init
SwsContext *ctx = sws_getContext(...);
// convert RGB->YUV
sws_scale(ctx, ...);

but that ends up doing the conversion completely single-threaded. There is a "threads" parameter that you can set on the context, to make it be able to multi-thread the conversion operation. But that parameter has to be set at initialization time, which means you can no longer use sws_getContext(), and instead you have to initialize the context the hard way:

SwsContext *get_threaded_sws_context(int width,
                                     int height,
                                     AVPixelFormat src_format,
                                     AVPixelFormat dst_format)
{
  /* sws_getContext does not allow passing flags that ask for multi-threaded
   * scaling context, so do it the hard way. */
  SwsContext *c = sws_alloc_context();
  if (c == nullptr) {
    return nullptr;
  }
  av_opt_set_int(c, "srcw", width, 0);
  av_opt_set_int(c, "srch", height, 0);
  av_opt_set_int(c, "src_format", src_format, 0);
  av_opt_set_int(c, "dstw", width, 0);
  av_opt_set_int(c, "dsth", height, 0);
  av_opt_set_int(c, "dst_format", dst_format, 0);
  av_opt_set_int(c, "sws_flags", SWS_BICUBIC, 0);
  av_opt_set_int(c, "threads", BLI_system_thread_count(), 0);

  if (sws_init_context(c, nullptr, nullptr) < 0) {
    sws_freeContext(c);
    return nullptr;
  }

  return c;
}

And you’d think that’s enough? Haha, of course not. sws_scale() never does multi-threading internally. For that, you need to use sws_scale_frame() instead. And once you do, it crashes since it turns out that you have had created your AVFrame objects just a tiny bit wrong that was completely fine for sws_scale, but is very much not fine for sws_scale_frame since the latter tries to do various sorts of reference counting and whatnot.

Kids, do not design APIs like this!

So all that took a while to figure out, but phew, done (#116008), and the RGB→YUV conversion step while writing a movie file is quite a bit faster now. And then do the same in the other direction, i.e. when reading a movie file, use multi-threaded YUV→RGB conversion, and fold vertical flip into the same operation as well (#116309).

Audio resampling

While looking at where time is spent while rendering a movie out of VSE, I noticed a this feels excessive moment where almost half of the time that takes to “produce a video or audio frame” is spent inside the audio library used by Blender (Audaspace). Not in encoding audio, just in mixing it before encoding! Turns out, most of that time is spent in resampling audio clip data, for example the movie is set to 48kHz audio, but some of the audio strips are 44.1kHz or similar. I started to dig in.

Audaspace, the audio engine, had two modes that it could do sound resampling: for inside-blender playback, it was using Linear resampler, which just linearly interpolates between samples. For rendering a movie, it was using Julius O Smith’s algorithm with, what it feels like, “uhh, somewhat overkill” parameter sizes.

One way to look at resampler quality is to take a synthetic sound, e.g. one that has a single increasing frequency, resample it, and look at the spectrogram of it. Here’s a “sweeping frequencies” sound, resampled inside Audacity with “best”, “medium” and “low” resampling settings. What you want is the result that looks like the “best” one, i.e. as little additional frequencies introduced as possible.

Inside Blender, Audaspace was providing two options: rendering vs. preview playback. Rendering one is good spectrogram indeed, whereas preview, while being fast to compute resampling, does introduce a lot of extra frequencies.

What I have done, is add a new “medium” resampling quality setting to Audaspace that, as far as I can tell, produces pretty much the same result while being about 3x faster to calculate. And made Blender use that when rendering:

With that, rendering a portion (2000 frames) of Sprite Fright on Windows Ryzen 5950X PC went 92sec→73 sec (#116059). And I’ve learned a thing or two about audio resampling. Not bad!

Image transformations and filtering

Strips that produce a visual (images, movies, text, scenes, …) in Blender VSE can be transformed: positioned, rotated, scaled, and additional cropping can be applied. Whenever that happens, the image that is normally produced by the strip is transformed into a new one. All of that is done on the CPU, and was multi-threaded already.

Yet it had some issues/bugs, and parts of the code could be optimized a bit. Plus some other things could be done.

“Why all of that is done on the CPU?!” you might ask. Good question! Part of the reason is, that no one made it be done on the GPU. Another part, is that the CPU fallback still needs to exist (at least right now), for the use case of: user wants to render things on a render farm that has no GPU.

“Off by half a pixel” errors

The code had various “off by half a pixel” errors that in many cases cancel themselves out or are invisible. Until they are not. This is not too dissimilar to “half texel offset” things that everyone had to go through in DirectX 9 times when doing any sort of image postprocessing. Felt like youth again :)

E.g. scaling a tiny image up 16x using Nearest and Bilinear filtering, respectively:

The Bilinear filter shifts the image by half the source pixel! (there’s also magenta – which is background color here – sneaking in; about that later)

In the other direction, scaling this image down exactly by 2x using Bilinear filtering does no filtering at all!

So things like that (as well as other “off by something” errors in other filters) got fixed (#116628). And the images above look like this with Bilinear 16x upscaling and 2x downscaling:

Transparency border around Bilinear filtering

VSE had three filtering options in Blender 4.0 and earlier: Nearest, Bilinear and Subsampled3x3. Of those, only the Bilinear one was adding half a source texel worth of transparency around the resulting image. Which is somewhat visible if you are scaling your media up. Why this discrepancy, no one remembers at this point, but it was there “forever”, it seems.

There’s a similar issue in Blender (CPU) Compositor, where Bilinear sampling of something blends in “transparency” when right on the edge of an image, whereas Bicubic sampling does not. Again, no one remembers why, and that should be addressed by someone. Someday.

I removed that “blend into transparency” from bilinear filtering code that is used by VSE. However! A side effect of this transparency thing, is that if you do not scale your image but only rotate it, the edge does get some sort of anti-aliasing. Which it would be losing now, if just removing that from bilinear.

So instead of blending in transparency when filtering the source image, instead I apply some sort of “transparency anti-aliasing” to the edge pixels of the destination image (#117717).

Filtering additions and changes

Regular VSE strip transforms did not have a cubic filtering option (it only existed in the special Transform Effect strip), which sounded like a curious omission. And that led into a rabbit hole of trying to figure out what exactly does Blender mean when they say “bicubic”, as well as what other software means by “bicubic”. It’s quite a mess lol! See an interactive comparison I made here:
aras-p.info/img/misc/upsample_filter_comp_2024

Anyway, “Bicubic” everywhere within Blender actually means “Cubic B-Spline” filtering, i.e. Mitchell-Netravali filter with B=1, C=0 coefficients, also known as “no ringing, but lots of blur”. Whether that’s a good choice depends on use case and what do the images represent. For VSE specifically, it sounded like the usual “Mitchell” filter (B=C=1/3) might have been better. Here’s both of them for example:

Both kinds of cubic filtering are an option in VSE now (#117100, #117517).

For downscaling the image, Blender 3.5 added a “Subsampled 3x3” filter. What it actually is, is a box filter that is hardcoded to 3x3 size. Whether box filter is a good filter, is a question for another day. But for now at least, I made it not be hardcoded to fixed 3x3 size (#117584), since if you scale the image down by not 3x3, it kinda starts to break down. Here, downscaling this perspective grid by 4x on each axis: original image, downscaled with current Subsampled 3x3 filter, and downscaled with the adjusted Box filter. Slightly better:

All of that is a lot of choices for the user, TBH! So I added an “Auto” filter option (#117853), that is now the default for VSE strips. It automatically picks the “most appropriate” filter based on transform data:

• When there is no scaling or rotation: Nearest,
• When scaling up by more than 2x: Cubic Mitchell,
• When scaling down by more than 2x: Box,
• Otherwise: Bilinear.

Besides all that, the image filtering process got a bit faster:

• Get rid of virtual functions from the inner loop, and some SIMD for bilinear filtering (#115653),
• Simplify cubic filtering, and add some SIMD (#117100),
• Simplify math used by Box (née Subsampled3x3) filter (#117125),
• Fix “does a solid image that covers the whole screen, and so we can skip everything under it” optimization not working, when said image has scale (#117786).

As a practical example, on my PC having a single 1920x1080 image in a 3840x2160 project (scaled up 2x), using Bilinear filtering: drawing the whole sequencer preview area went from 36.8ms down to 15.9ms. I have some ideas how to speed it up further.

Optimizing VSE Effects

While the actual movie data sets I have from Blender Studio do not use much/any effects, I optimized them by noticing something in the code. Most of that is just multi-threading.

• Glow effect: multi-threaded now, 6x-10x faster (#115818).
• Wipe effect: multi-threaded now, and simplify excessive trigonometry in Clock wipe; 6x-20x faster (#115837).
• Gamma Cross effect: was doing really complex table + interpolation based things just to avoid a single square root call. Felt like the code was written before hardware floating point was invented :) 4x faster now (#115801).
• Gaussian Blur effect: 1.5x faster by avoiding some redundant calculations (#116089).

What does all of that mean for render times?

On the three data sets I have from Blender Studio, the final render time of a VSE movie is about 2x faster on my PC. For example, the same Sprite Fright edit: rendering it went from almost 13 minutes down to 7 minutes.

I hope things can be further sped up. We “only” need to do 2x speedup another three times, and then it’s quite good, right? :P

Thoughts on actual work process

Is all of the above a “good amount of work” done, for two months part-time effort?

I don’t know. I think it’s quite okay, especially considering that the developer (me) knew nothing about the area or the codebase. Besides the user-visible changes outlined above, I did a handful of pull requests that were adding tests, refactoring code, cleaning something up, etc. In total 37 pull requests got done, reviewed and merged.

And here’s the interesting bit: I’m pretty sure I could have not done this at an “actual job”. I don’t have many jobs to compare, but e.g. at Unity between around 2015 and 2022, I think I would have been able to do like 30% of the above in the same time. Maybe less. I probably could have done the above at “ancient” Unity, i.e. around year 2010 or so.

The reasons are numerous and complex, and have to do with amount of people within the company, processes, expectations, communication, politics and whatnot. But it is weirdly funny, that if I’m able to do “X amount of work in Y amount of time” for free, then at a company where it would pay me relatively lotsa money for the work, various forces would try to make me do the same work slower. Or not finish the work at all, since due to (again, complex reasons) the effort might get cancelled midway!

I hope Blender does not venture into that size/complexity/workflow where it feels like The Process is not helping, but rather is there to demotivate and slow down everyone (not on purpose! it just slowly becomes that way).

What’s next?

Who knows! Blender 4.1 just became beta, which means feature-wise, it is “done” and the VSE related bits in 4.1 are going to be as they are right now.

However, work on Blender 4.2 starts now, and then 4.3, … For the near future, I want to keep tinkering with it. But without a clear plan :) Once I have something done, maybe I’ll write about them. Meanwhile, things can be observed in the Weekly Updates forum section.

Until next time! Happy video sequence editing!