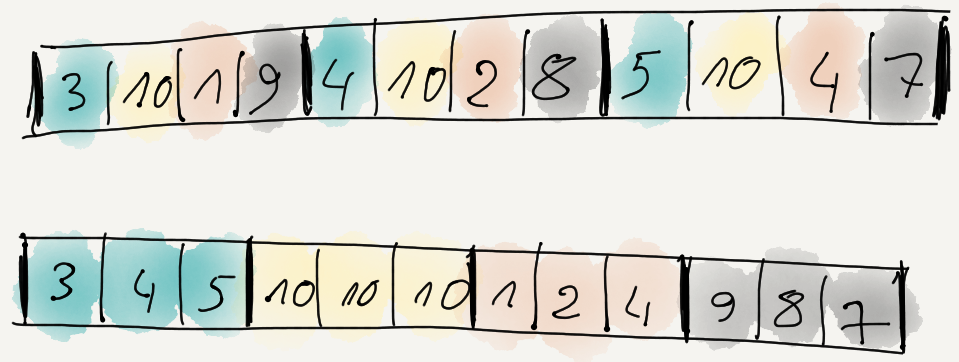Introduction and index of this series is here.
Several posts ago we learned that filtering the data can make it more compressible. Out of
several simple filters that I tried, “reorder data items byte-wise and delta encode that” was the most effective at improving compression ratio.
That’s all nice and good, but the filtering has a cost to it. One is the extra memory needed to hold the filtered data, and another is
the time it takes to do the filtering. While for compression the relative speed hit is fairly small (i.e. compression itself takes much longer),
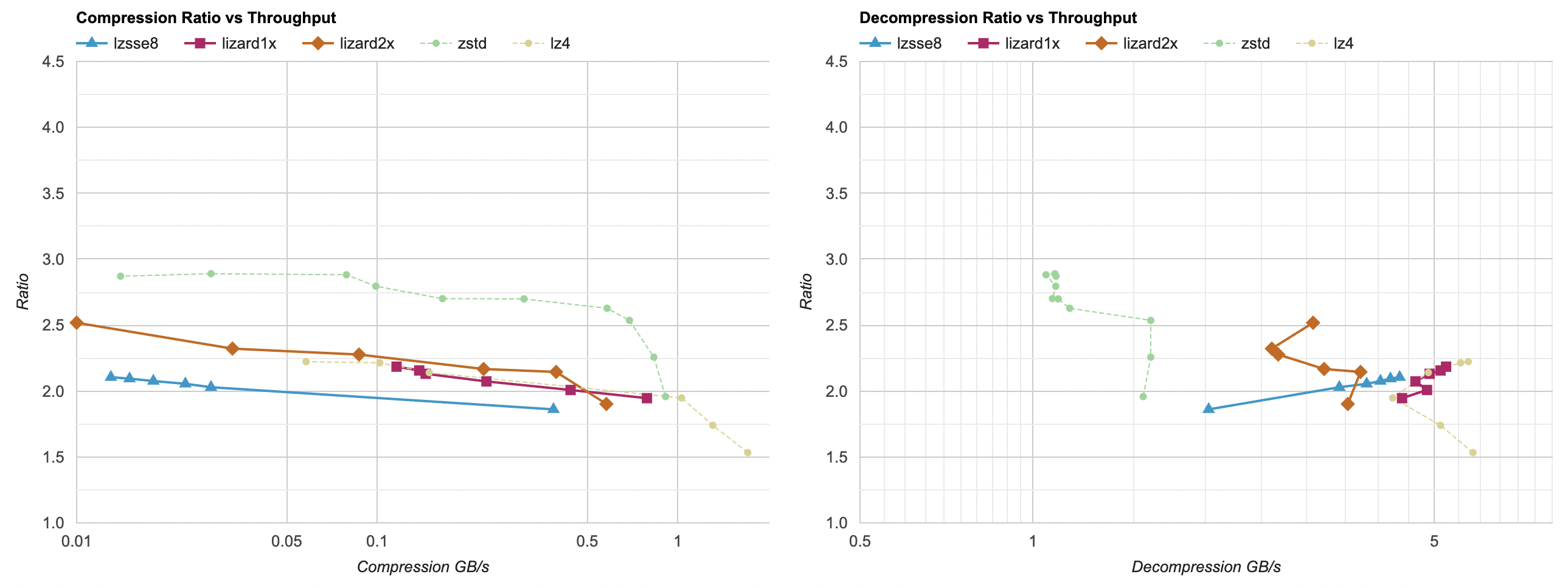
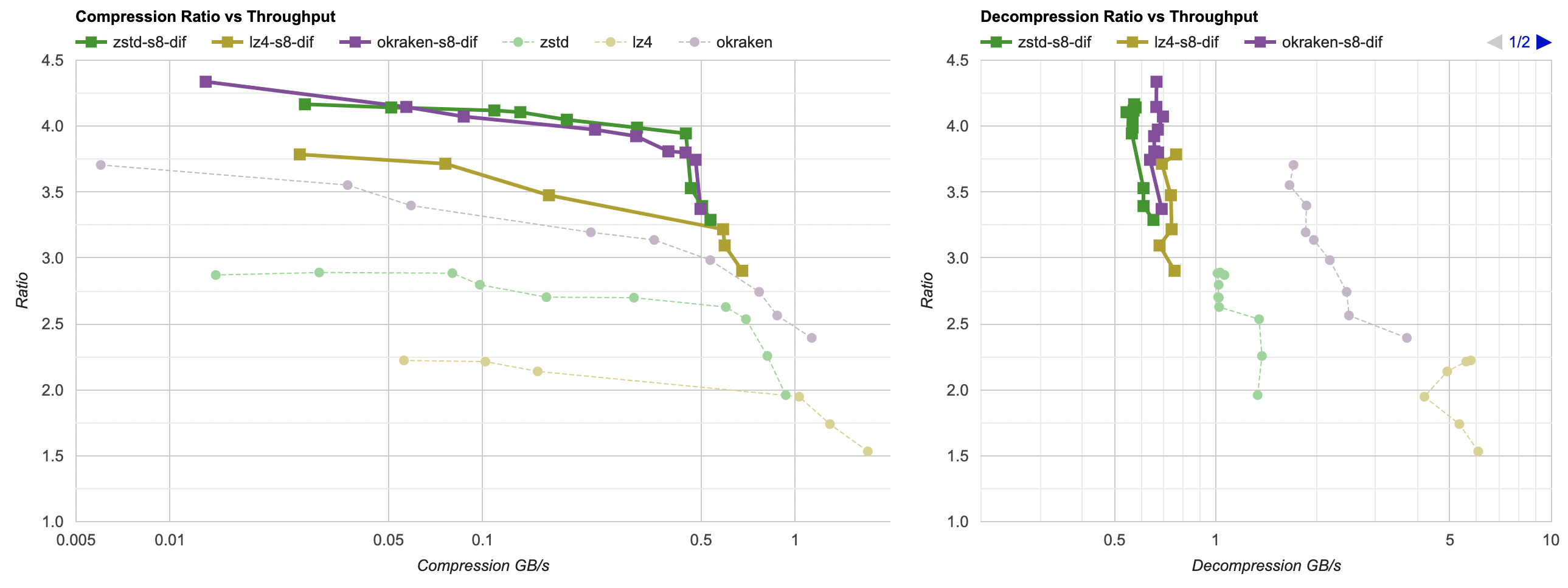
for decompression the cost is not trivial. A fast decompressor like LZ4 normally goes at ~5GB/s, but with “reorder bytes + delta” filter
it only achieves 0.8GB/s:
Can we do something simple (i.e. something even me could do) to speed that up a bit? Let’s find out.
Decompression filter optimization
The code we are starting with is this: first decode the delta-encoded data, then un-split the data items, i.e. assemble the items
from the “first byte of each item, then 2nd byte of each item, then 3rd byte of each item” layout. Like this:
// channels: how many items per data element
// dataElems: how many data elements
template<typename T>
static void UnSplit(const T* src, T* dst, int channels, size_t dataElems)
{
for (int ich = 0; ich < channels; ++ich)
{
T* dstPtr = dst + ich;
for (size_t ip = 0; ip < dataElems; ++ip)
{
*dstPtr = *src;
src += 1;
dstPtr += channels;
}
}
}
template<typename T>
static void DecodeDeltaDif(T* data, size_t dataElems)
{
T prev = 0;
for (size_t i = 0; i < dataElems; ++i)
{
T v = *data;
v = prev + v;
*data = v;
prev = v;
++data;
}
}
void UnSplit8Delta(uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
DecodeDeltaDif<uint8_t>(src, channels * dataElems);
UnSplit<uint8_t>(src, dst, channels, dataElems);
}
Now, this process does not depend on the compression library or the settings used for it; it’s always the same for all of them. So instead of complicated
per-compressor scatter plots I’ll just give three time numbers: milliseconds that it takes to do the filtering process on our 94.5MB data set.
Two numbers on Windows PC (Ryzen 5950X, Visual Studio 2022 16.4 and Clang 15.0), and one on a Mac laptop (Apple M1 Max, Apple Clang 14.0).
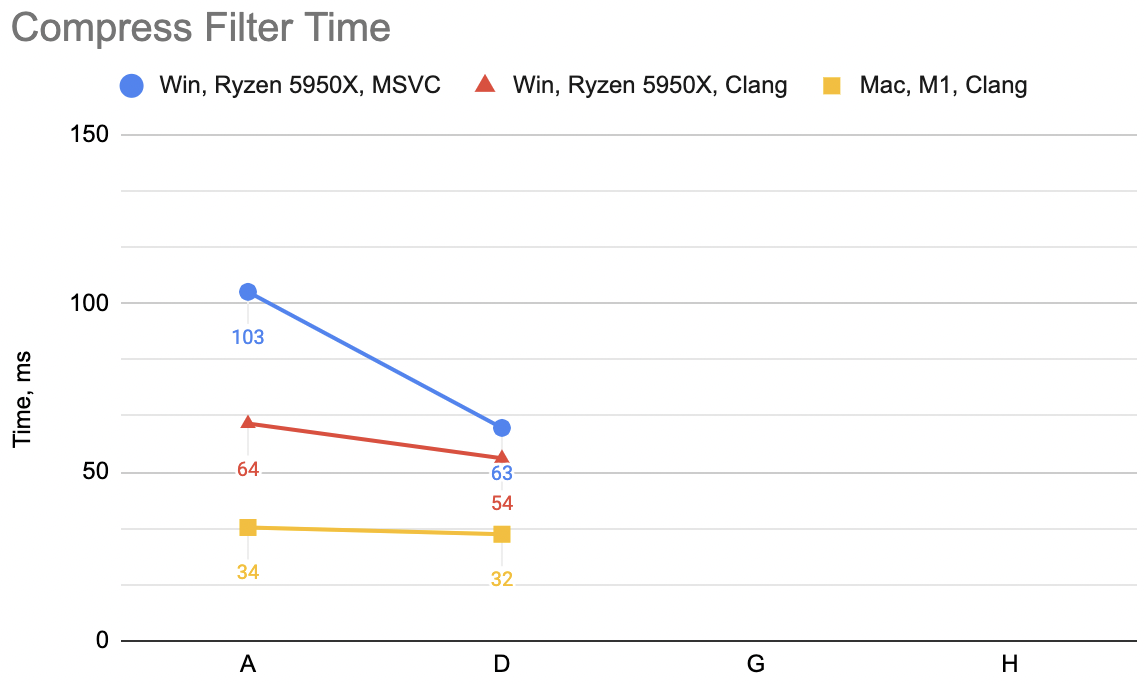
The code above, which I’m gonna label “A”: WinVS 27.9ms, WinClang 29.7ms, MacClang 23.9ms.
Attempt B: combine unsplit+delta into one
The code above does two passes over the data: first the delta-decode, then the un-split. This is good for “code reuse”, as in arbitrarily
complex filters can be produced by combining several simple filters in sequence. But if we know we already locked onto “split bytes + delta”,
then we can try combining all that into just once function:
void UnSplit8Delta(uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev = 0;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t* dstPtr = dst + ich;
for (size_t ip = 0; ip < dataElems; ++ip)
{
uint8_t v = *src + prev;
prev = v;
*dstPtr = v;
src += 1;
dstPtr += channels;
}
}
}
“B”: WinVS 19.5ms, WinClang 18.9ms, MacClang 9.5ms (“A” was: 27.9, 29.7, 23.9). Not bad at all, and the code is actually smaller now.
Attempt C: I heard something about SIMD
CPUs these days have this “SIMD” thing, and for usual use cases we
can pretty much assume that something like SSE4 is available on Intel architectures, and
NEON on ARM architectures. Our
code loops over data “quite a lot”, doing very simple operations with it. Would trying to sprinkle some manually written SIMD in there
help?
One spanner in the works is that the loop in there is not independent operations: each iteration of the loop updates the prev byte value.
Delta-encoded data decoding is essentially a prefix sum operation, and some five minute googling
having been aware of all of Fabian’s tweets and toots, ever finds this gist
with a prefix_sum_u8 function for SSE. So with that, let’s try to rewrite the above code so that the inner loop can do
16 bytes at a time, for both SSE and NEON cases.
The code’s quite a bit longer:
#if defined(__x86_64__) || defined(_M_X64)
# define CPU_ARCH_X64 1
# include <emmintrin.h> // sse2
# include <tmmintrin.h> // sse3
# include <smmintrin.h> // sse4.1
#endif
#if defined(__aarch64__) || defined(_M_ARM64)
# define CPU_ARCH_ARM64 1
# include <arm_neon.h>
#endif
#if CPU_ARCH_X64
// https://gist.github.com/rygorous/4212be0cd009584e4184e641ca210528
static inline __m128i prefix_sum_u8(__m128i x)
{
x = _mm_add_epi8(x, _mm_slli_epi64(x, 8));
x = _mm_add_epi8(x, _mm_slli_epi64(x, 16));
x = _mm_add_epi8(x, _mm_slli_epi64(x, 32));
x = _mm_add_epi8(x, _mm_shuffle_epi8(x, _mm_setr_epi8(-1,-1,-1,-1,-1,-1,-1,-1,7,7,7,7,7,7,7,7)));
return x;
}
#endif // #if CPU_ARCH_X64
#if CPU_ARCH_ARM64
// straight-up port to NEON of the above; no idea if this is efficient at all, yolo!
static inline uint8x16_t prefix_sum_u8(uint8x16_t x)
{
x = vaddq_u8(x, vshlq_u64(x, vdupq_n_u64(8)));
x = vaddq_u8(x, vshlq_u64(x, vdupq_n_u64(16)));
x = vaddq_u8(x, vshlq_u64(x, vdupq_n_u64(32)));
alignas(16) uint8_t tbl[16] = {0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,7,7,7,7,7,7,7,7};
x = vaddq_u8(x, vqtbl1q_u8(x, vld1q_u8(tbl)));
return x;
}
#endif // #if CPU_ARCH_ARM64
void UnSplit8Delta(uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev = 0;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t* dstPtr = dst + ich;
size_t ip = 0;
# if CPU_ARCH_X64
// SSE simd loop, 16 bytes at a time
__m128i prev16 = _mm_set1_epi8(prev);
__m128i hibyte = _mm_set1_epi8(15);
alignas(16) uint8_t scatter[16];
for (; ip < dataElems / 16; ++ip)
{
// load 16 bytes of filtered data
__m128i v = _mm_loadu_si128((const __m128i*)src);
// un-delta via prefix sum
prev16 = _mm_add_epi8(prefix_sum_u8(v), _mm_shuffle_epi8(prev16, hibyte));
// scattered write into destination
_mm_store_si128((__m128i*)scatter, prev16);
for (int lane = 0; lane < 16; ++lane)
{
*dstPtr = scatter[lane];
dstPtr += channels;
}
src += 16;
}
prev = _mm_extract_epi8(prev16, 15); // sse4.1
# endif // if CPU_ARCH_X64
# if CPU_ARCH_ARM64
// NEON simd loop, 16 bytes at a time
uint8x16_t prev16 = vdupq_n_u8(prev);
uint8x16_t hibyte = vdupq_n_u8(15);
alignas(16) uint8_t scatter[16];
for (; ip < dataElems / 16; ++ip)
{
// load 16 bytes of filtered data
uint8x16_t v = vld1q_u8(src);
// un-delta via prefix sum
prev16 = vaddq_u8(prefix_sum_u8(v), vqtbl1q_u8(prev16, hibyte));
// scattered write into destination
vst1q_u8(scatter, prev16);
for (int lane = 0; lane < 16; ++lane)
{
*dstPtr = scatter[lane];
dstPtr += channels;
}
src += 16;
}
prev = vgetq_lane_u8(prev16, 15);
# endif // if CPU_ARCH_ARM64
// any trailing leftover
for (ip = ip * 16; ip < dataElems; ++ip)
{
uint8_t v = *src + prev;
prev = v;
*dstPtr = v;
src += 1;
dstPtr += channels;
}
}
}
Phew. “C”: WinVS 19.7ms, WinClang 18.7ms, MacClang 8.3ms (“B” was: 19.5, 18.9, 9.5). Meh! 😕 This makes
the Apple/NEON case a bit faster, but on PC/SSE case it’s pretty much the same timings.
Lesson: just because you use some SIMD, does not necessarily make things faster. In this
case, I suspect it’s the lack of independent work that’s available (each loop iteration
depends on results of previous iteration; and “work” within loop is tiny), and the scattered
memory writes are the problem. If I was less lazy I’d try to draw up
a data flow graph
or something.
Attempt D: undeterred, even more SIMD
The SIMD attempt was a lot of code for very little (if any) gain, but hey what if we try adding even more SIMD?
Looking at the assembly of the compiled code in compiler explorer, I noticed that
while while Clang can keep code like this:
// scattered write into destination
_mm_store_si128((__m128i*)scatter, prev16);
for (int lane = 0; lane < 16; ++lane)
{
*dstPtr = scatter[lane];
dstPtr += channels;
}
completely within SIMD registers, MSVC can not. Clang compiles the above into a sequence of
pextrb (SSE) and st1 (NEON)
instructions, like:
; SSE
pextrb byte ptr [rbx], xmm3, 0
pextrb byte ptr [rbx + rax], xmm3, 1
add rbx, rax
pextrb byte ptr [rax + rbx], xmm3, 2
add rbx, rax
pextrb byte ptr [rax + rbx], xmm3, 3
add rbx, rax
; ...
; NEON
st1 { v2.b }[0], [x13]
add x13, x15, x8
st1 { v2.b }[1], [x12]
add x12, x13, x8
st1 { v2.b }[2], [x15]
add x15, x12, x8
; ...
But MSVC is emitting assembly very similar to how the code is written: first writes the SSE register
into memory, and then stores each byte of that into final location:
movdqa XMMWORD PTR scatter$1[rsp], xmm3
movdqa xmm0, xmm3
psrldq xmm0, 8
movd ecx, xmm3
mov BYTE PTR [rax], cl
add rax, rbx
movzx ecx, BYTE PTR scatter$1[rsp+1]
mov BYTE PTR [rax], cl
add rax, rbx
movzx ecx, BYTE PTR scatter$1[rsp+2]
mov BYTE PTR [rax], cl
add rax, rbx
movzx ecx, BYTE PTR scatter$1[rsp+3]
mov BYTE PTR [rax], cl
add rax, rbx
; ...
So how about if we replace that loop with a sequence of _mm_extract_epi8 (SSE intrinsic function that maps to pextrb)?
// scattered write into destination
//_mm_store_si128((__m128i*)scatter, prev16);
//for (int lane = 0; lane < 16; ++lane)
//{
// *dstPtr = scatter[lane];
// dstPtr += channels;
//}
*dstPtr = _mm_extract_epi8(prev16, 0); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 1); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 2); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 3); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 4); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 5); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 6); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 7); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 8); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 9); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 10); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 11); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 12); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 13); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 14); dstPtr += channels;
*dstPtr = _mm_extract_epi8(prev16, 15); dstPtr += channels;
And a very similar thing could be done for NEON, just each line would look
like *dstPtr = vgetq_lane_u8(prev16, 0); dstPtr += channels; and so on. And now MSVC does keep everything within SIMD registers. There’s no
change on Clang, either in SSE nor NEON case.
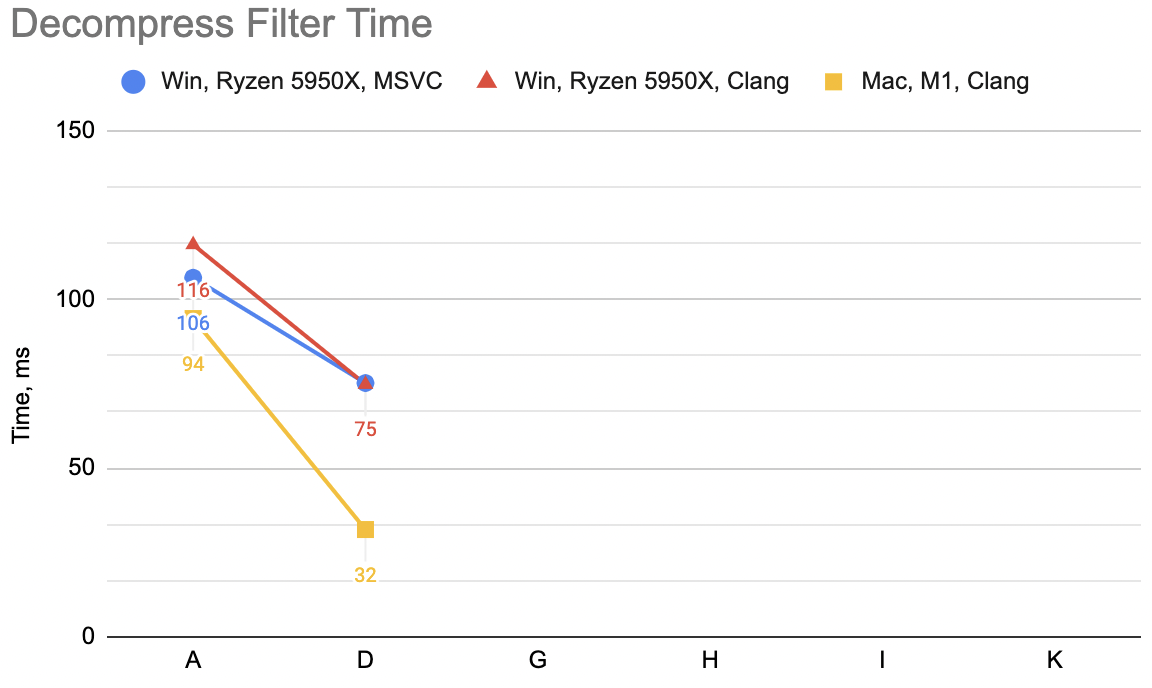
“D”: WinVS 18.8ms, WinClang 18.8ms, MacClang 8.3ms (“B” was: 19.7, 18.7, 8.3). Ok, a small improvement for MSVC,
unchanged (as expected) for the two Clang cases.
Attempt E: try to flip it around
Ok so that whole SIMD thing was a lot of code for very little gain. How about something different? Our UnSplit8Delta reads the source
data sequentially, but does “scattered” writes into destination array. How about if we change the order, so that the destination
writes are done sequentially, but the source data is “gathered” from multiple locations?
This is not easily done due to delta decoding that needs to happen, so we’ll just first do delta-decoding in place (modifying the source
array! YOLO!), and then to the “unsplit” part. Upper part of the code (prefix_sum_u8 etc.) as before; the function itself now is:
void UnSplit8Delta(uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
// first pass: decode delta
const size_t dataSize = dataElems * channels;
uint8_t* ptr = src;
size_t ip = 0;
uint8_t prev = 0;
# if CPU_ARCH_X64
// SSE simd loop, 16 bytes at a time
__m128i prev16 = _mm_set1_epi8(0);
__m128i hibyte = _mm_set1_epi8(15);
for (; ip < dataSize / 16; ++ip)
{
__m128i v = _mm_loadu_si128((const __m128i*)ptr);
// un-delta via prefix sum
prev16 = _mm_add_epi8(prefix_sum_u8(v), _mm_shuffle_epi8(prev16, hibyte));
_mm_storeu_si128((__m128i*)ptr, prev16);
ptr += 16;
}
prev = _mm_extract_epi8(prev16, 15); // sse4.1
# endif // if CPU_ARCH_X64
# if CPU_ARCH_ARM64
// NEON simd loop, 16 bytes at a time
uint8x16_t prev16 = vdupq_n_u8(prev);
uint8x16_t hibyte = vdupq_n_u8(15);
for (; ip < dataSize / 16; ++ip)
{
uint8x16_t v = vld1q_u8(ptr);
// un-delta via prefix sum
prev16 = vaddq_u8(prefix_sum_u8(v), vqtbl1q_u8(prev16, hibyte));
vst1q_u8(ptr, prev16);
ptr += 16;
}
prev = vgetq_lane_u8(prev16, 15);
# endif // if CPU_ARCH_ARM64
// any trailing leftover
for (ip = ip * 16; ip < dataSize; ++ip)
{
uint8_t v = *ptr + prev;
prev = v;
*ptr = v;
ptr += 1;
}
// second pass: un-split; sequential write into destination
uint8_t* dstPtr = dst;
for (int ip = 0; ip < dataElems; ++ip)
{
const uint8_t* srcPtr = src + ip;
for (int ich = 0; ich < channels; ++ich)
{
uint8_t v = *srcPtr;
*dstPtr = v;
srcPtr += dataElems;
dstPtr += 1;
}
}
}
Times for “E”: WinVS 20.9ms, WinClang 14.3ms, MacClang 16.3ms (“C” was: 18.8, 18.8, 8.3). Now that is curious! The two
“primary” configurations (Windows MSVC and Mac Clang) get slower or much slower. You could have expected that; this function
gets us back into “two passes over memory” land. But the Windows Clang gets quite a bit faster 🤔
Looking at the code in compiler explorer, Clang for x64 decides to unroll the un-split loop into
a loop that does 8 bytes at a time; whereas MSVC x64 and Clang arm64 does a simple loop of one byte at a time, as written in C code.
However I know my data; and I know that majority of my data is 16-byte data items. But, trying to explicitly add a code path for channels==16
case, and manually unrolling the loop to do 16 bytes at a time gets slower. Maybe something to look into some other day.
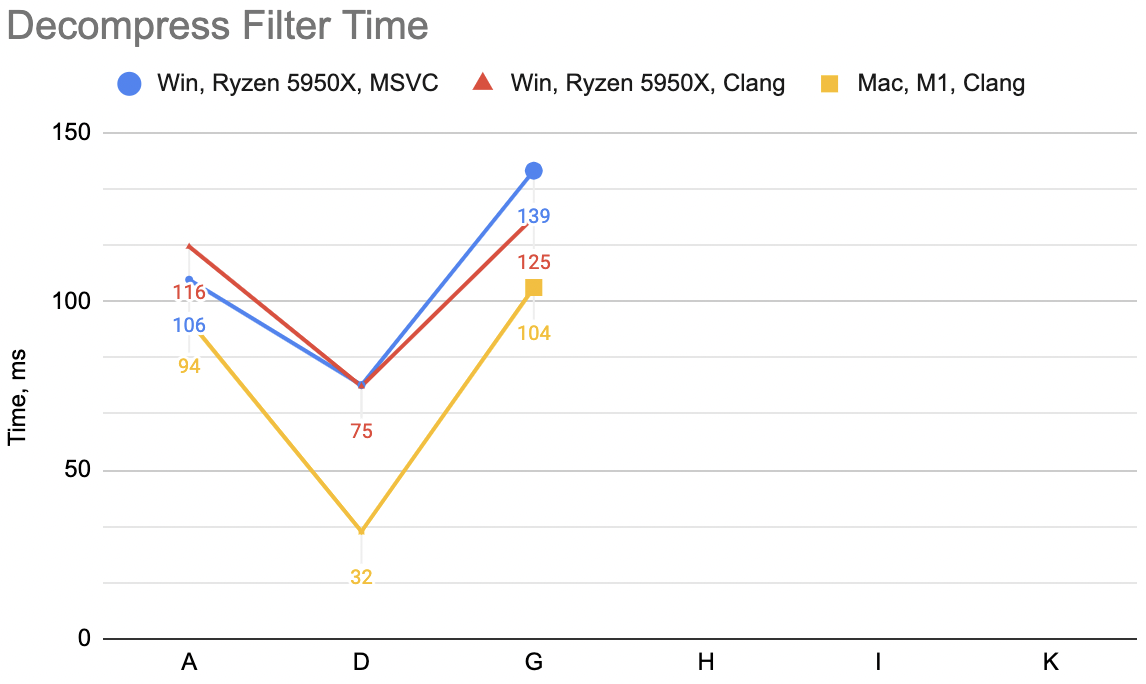
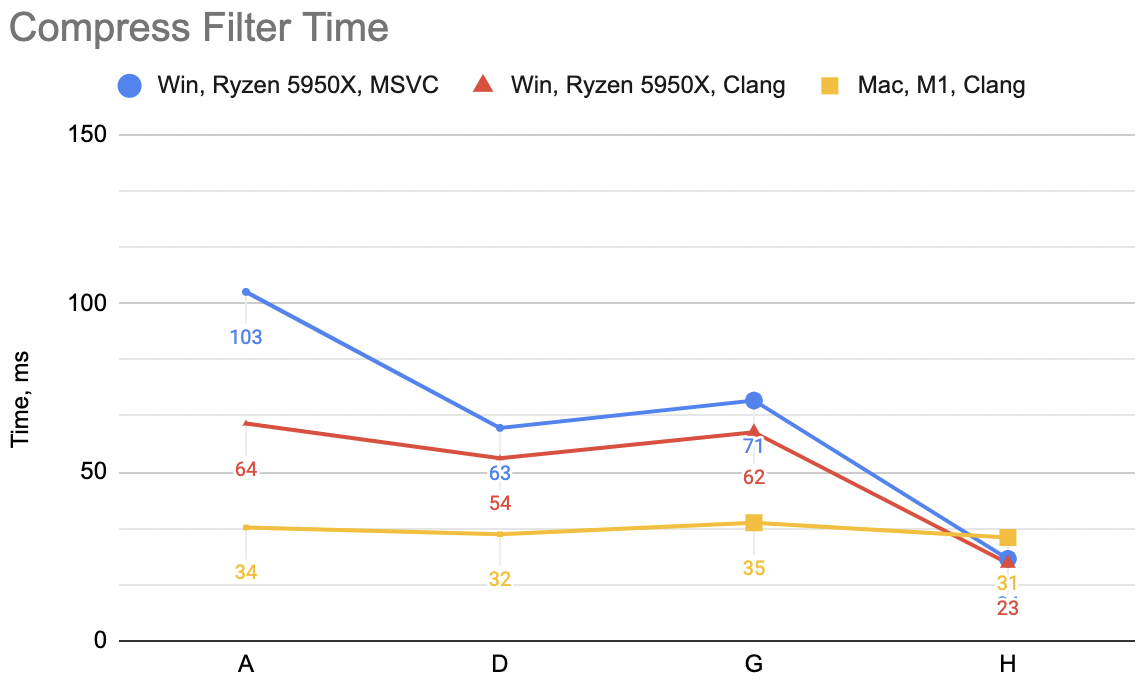
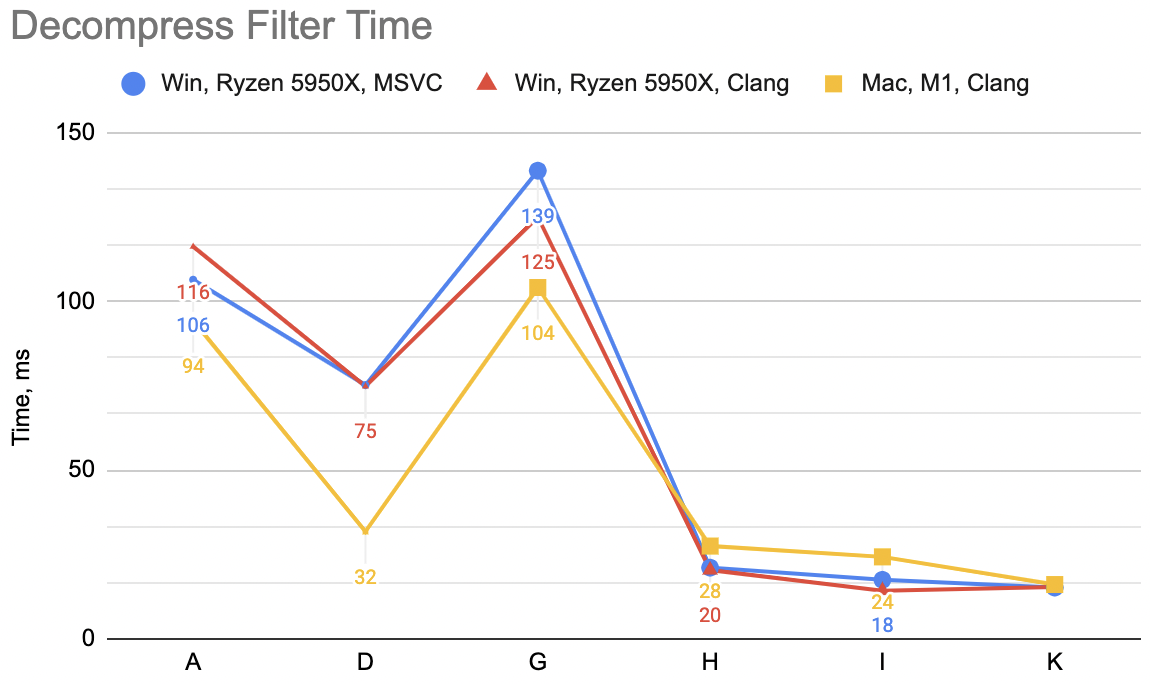
For now I’ll say it’s enough of decoding speedup attempts. We are here:
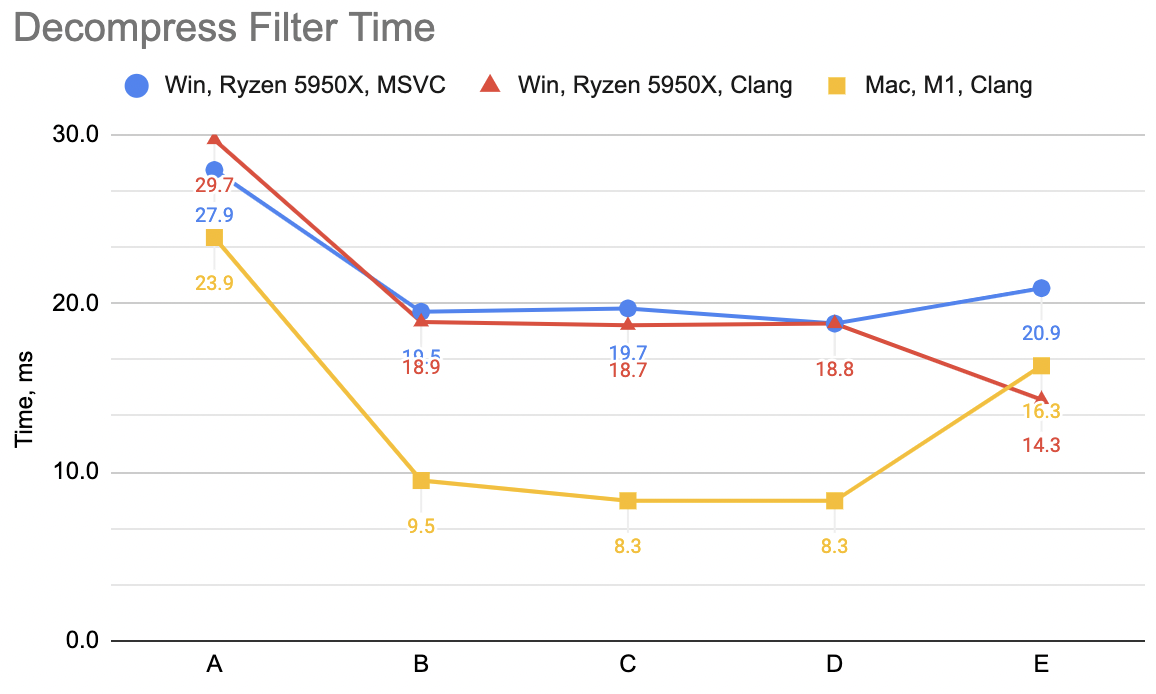
And the lesson so far is, that the most trivial of code changes (just fold delta + unsplit into one function, with one pass over memory)
got the largest speedup – from 24..30ms depending on the platform, the time went down to 10..20ms.
Additional SIMD things can get it a bit faster, but I suspect if we’re looking for larger gains, we’d want to change the filter itself,
so that it is no longer just one “stream” of delta bytes, but rather perhaps several interleaved streams. That way, all the fancy
machinery inside CPUs that can do kphjillion operations in parallel can actually do it.
Compression filter optimization
While compression filter cost is relatively cheap compared to the lossless compression part itself, I did very similar attempts at speeding that
one up. A short run through these is below. We start with “split data, delta encode” as two passes over memory:
template<typename T>
static void EncodeDeltaDif(T* data, size_t dataElems)
{
T prev = 0;
for (size_t i = 0; i < dataElems; ++i)
{
T v = *data;
*data = v - prev;
prev = v;
++data;
}
}
template<typename T>
static void Split(const T* src, T* dst, int channels, size_t dataElems)
{
for (int ich = 0; ich < channels; ++ich)
{
const T* ptr = src + ich;
for (size_t ip = 0; ip < dataElems; ++ip)
{
*dst = *ptr;
ptr += channels;
dst += 1;
}
}
}
void Split8Delta(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
Split<uint8_t>(src, dst, channels, dataElems);
EncodeDeltaDif<uint8_t>(dst, channels * dataElems);
}
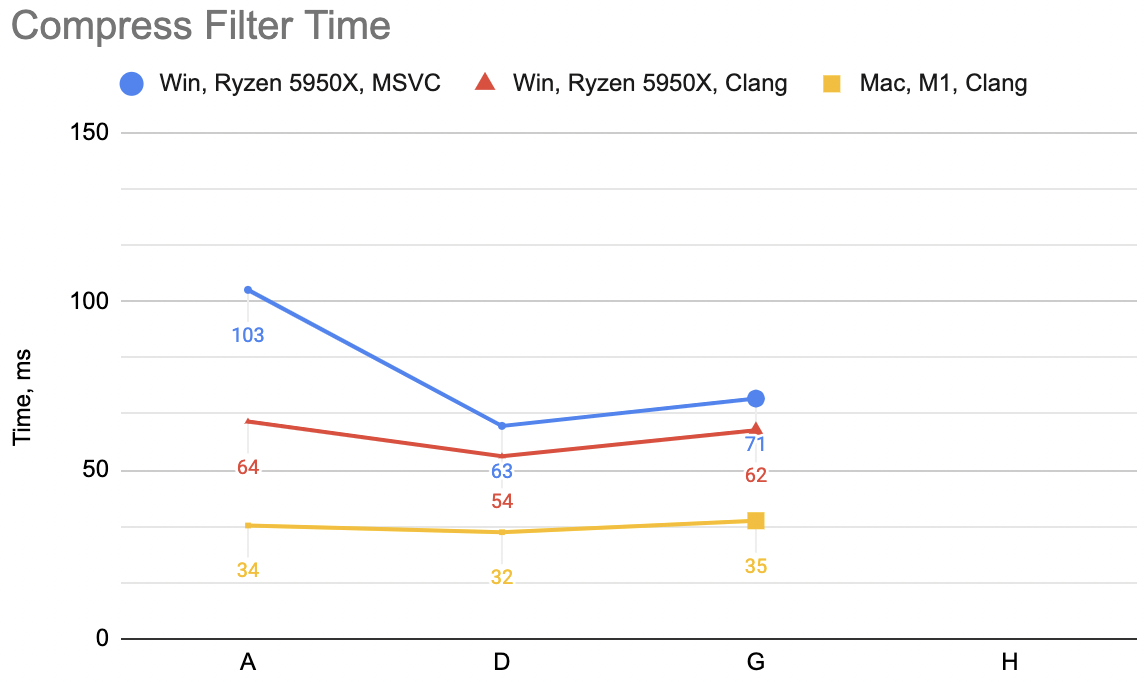
Which is “A”: WinVS 27.6ms, WinClang 17.9ms, MacClang 9.6ms.
Next up, fold split and delta into one function:
void Split8Delta(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev = 0;
for (int ich = 0; ich < channels; ++ich)
{
const uint8_t* srcPtr = src + ich;
for (size_t ip = 0; ip < dataElems; ++ip)
{
uint8_t v = *srcPtr;
*dst = v - prev;
prev = v;
srcPtr += channels;
dst += 1;
}
}
}
Which is “B”: WinVS 21.0ms, WinClang 18.0ms, MacClang 11.0ms (“A” was: 27.6, 17.9, 9.6). Curious! WinVS a good chunk faster,
WinClang unchanged, MacClang a bit slower. This is very different from the decoding filter case!
Ok, throw in some SIMD, very much like above. Process data 16 bytes at a time, with a scalar loop at the end for any leftovers:
#if defined(__x86_64__) || defined(_M_X64)
# define CPU_ARCH_X64 1
# include <emmintrin.h> // sse2
# include <tmmintrin.h> // sse3
# include <smmintrin.h> // sse4.1
#endif
#if defined(__aarch64__) || defined(_M_ARM64)
# define CPU_ARCH_ARM64 1
# include <arm_neon.h>
#endif
void Split8Delta(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev = 0;
for (int ich = 0; ich < channels; ++ich)
{
const uint8_t* srcPtr = src + ich;
size_t ip = 0;
# if CPU_ARCH_X64
// SSE simd loop, 16 bytes at a time
__m128i prev16 = _mm_set1_epi8(prev);
alignas(16) uint8_t gathered[16];
for (; ip < dataElems / 16; ++ip)
{
// gather 16 bytes from source data
for (int lane = 0; lane < 16; ++lane)
{
gathered[lane] = *srcPtr;
srcPtr += channels;
}
__m128i v = _mm_load_si128((const __m128i*)gathered);
// delta from previous
__m128i delta = _mm_sub_epi8(v, _mm_alignr_epi8(v, prev16, 15)); // sse3
_mm_storeu_si128((__m128i*)dst, delta);
prev16 = v;
dst += 16;
}
prev = _mm_extract_epi8(prev16, 15); // sse4.1
# endif // if CPU_ARCH_X64
# if CPU_ARCH_ARM64
// NEON simd loop, 16 bytes at a time
uint8x16_t prev16 = vdupq_n_u8(prev);
alignas(16) uint8_t gathered[16];
for (; ip < dataElems / 16; ++ip)
{
// gather 16 bytes from source data
for (int lane = 0; lane < 16; ++lane)
{
gathered[lane] = *srcPtr;
srcPtr += channels;
}
uint8x16_t v = vld1q_u8(gathered);
// delta from previous
uint8x16_t delta = vsubq_u8(v, vextq_u8(prev16, v, 15));
vst1q_u8(dst, delta);
prev16 = v;
dst += 16;
}
prev = vgetq_lane_u8(prev16, 15);
# endif // if CPU_ARCH_ARM64
// any trailing leftover
for (ip = ip * 16; ip < dataElems; ++ip)
{
uint8_t v = *srcPtr;
*dst = v - prev;
prev = v;
srcPtr += channels;
dst += 1;
}
}
}
Which is “C”: WinVS 18.0ms, WinClang 18.3ms, MacClang 17.5ms (“B” was: 21.0, 18.0, 11.0). Hmm. MSVC keeps on improving, Windows Clang
stays the same, Mac Clang gets a lot slower. Eek!
Undeterred, I’m going to do another attempt, just like for decompression above: replace the data gather loop written in C:
for (int lane = 0; lane < 16; ++lane)
{
gathered[lane] = *srcPtr;
srcPtr += channels;
}
with one that uses SIMD intrinsics instead:
void Split8Delta(const uint8_t* src, uint8_t* dst, int channels, size_t dataElems)
{
uint8_t prev = 0;
for (int ich = 0; ich < channels; ++ich)
{
const uint8_t* srcPtr = src + ich;
size_t ip = 0;
# if CPU_ARCH_X64
// SSE simd loop, 16 bytes at a time
__m128i prev16 = _mm_set1_epi8(prev);
for (; ip < dataElems / 16; ++ip)
{
// gather 16 bytes from source data
__m128i v = _mm_set1_epi8(0);
v = _mm_insert_epi8(v, *srcPtr, 0); srcPtr += channels; // sse4.1
v = _mm_insert_epi8(v, *srcPtr, 1); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 2); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 3); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 4); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 5); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 6); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 7); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 8); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 9); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 10); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 11); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 12); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 13); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 14); srcPtr += channels;
v = _mm_insert_epi8(v, *srcPtr, 15); srcPtr += channels;
// delta from previous
__m128i delta = _mm_sub_epi8(v, _mm_alignr_epi8(v, prev16, 15)); // sse3
_mm_storeu_si128((__m128i*)dst, delta);
prev16 = v;
dst += 16;
}
prev = _mm_extract_epi8(prev16, 15); // sse4.1
# endif // if CPU_ARCH_X64
# if CPU_ARCH_ARM64
// NEON simd loop, 16 bytes at a time
uint8x16_t prev16 = vdupq_n_u8(prev);
for (; ip < dataElems / 16; ++ip)
{
// gather 16 bytes from source data
uint8x16_t v = vdupq_n_u8(0);
v = vsetq_lane_u8(*srcPtr, v, 0); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 1); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 2); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 3); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 4); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 5); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 6); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 7); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 8); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 9); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 10); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 11); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 12); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 13); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 14); srcPtr += channels;
v = vsetq_lane_u8(*srcPtr, v, 15); srcPtr += channels;
// delta from previous
uint8x16_t delta = vsubq_u8(v, vextq_u8(prev16, v, 15));
vst1q_u8(dst, delta);
prev16 = v;
dst += 16;
}
prev = vgetq_lane_u8(prev16, 15);
# endif // if CPU_ARCH_ARM64
// any trailing leftover
for (ip = ip * 16; ip < dataElems; ++ip)
{
uint8_t v = *srcPtr;
*dst = v - prev;
prev = v;
srcPtr += channels;
dst += 1;
}
}
}
Which now is “D”: WinVS 17.5ms, WinClang 15.2ms, MacClang 9.1ms (“C” was: 18.0, 18.3, 17.5). Whoa. This is the fastest version now,
and Mac especially got out of that strange slowness from “C” case. But how and why?
The NEON assembly of gather loop in “C” case was like:
.LBB0_10:
add x12, x0, x9
mov x14, x10
dup v1.16b, w13
.LBB0_11:
ld1 { v0.b }[0], [x12], x8
subs x14, x14, #1
ld1 { v0.b }[1], [x12], x8
ld1 { v0.b }[2], [x12], x8
ld1 { v0.b }[3], [x12], x8
ld1 { v0.b }[4], [x12], x8
ld1 { v0.b }[5], [x12], x8
ld1 { v0.b }[6], [x12], x8
ld1 { v0.b }[7], [x12], x8
ld1 { v0.b }[8], [x12], x8
ld1 { v0.b }[9], [x12], x8
ld1 { v0.b }[10], [x12], x8
ld1 { v0.b }[11], [x12], x8
ld1 { v0.b }[12], [x12], x8
ld1 { v0.b }[13], [x12], x8
ld1 { v0.b }[14], [x12], x8
ext v1.16b, v1.16b, v0.16b, #15
; ...
i.e. it’s a series of one-byte loads into each byte-wide lane of a NEON register. Cool. The assembly of “D” case, which is twice as fast, is:
.LBB0_10:
add x12, x0, x9
mov x14, x10
dup v0.16b, w13
.LBB0_11:
movi v1.2d, #0000000000000000
subs x14, x14, #1
ld1 { v1.b }[0], [x12], x8
ld1 { v1.b }[1], [x12], x8
ld1 { v1.b }[2], [x12], x8
ld1 { v1.b }[3], [x12], x8
ld1 { v1.b }[4], [x12], x8
ld1 { v1.b }[5], [x12], x8
ld1 { v1.b }[6], [x12], x8
ld1 { v1.b }[7], [x12], x8
ld1 { v1.b }[8], [x12], x8
ld1 { v1.b }[9], [x12], x8
ld1 { v1.b }[10], [x12], x8
ld1 { v1.b }[11], [x12], x8
ld1 { v1.b }[12], [x12], x8
ld1 { v1.b }[13], [x12], x8
ld1 { v1.b }[14], [x12], x8
ext v0.16b, v0.16b, v1.16b, #15
; ...
it’s the same series of one-byte loads into a NEON register! What gives?!
The movi v1.2d, #0000000000000000 is the key. In my hand-written NEON intrinsics version, I have for some reason wrote it in
a way that first sets the whole register to zero: uint8x16_t v = vdupq_n_u8(0); and then proceeds to load each byte of it.
Whereas in the C version, there’s a alignas(16) uint8_t gathered[16]; variable outside the loop, and nothing tells the compiler or
the CPU that it’s completely overwritten on each loop iteration. This, I guess, creates a dependency between loop iterations where
some sort of register renaming whatever can not kick in.
Knowing that, we could get back to a version written in C, and on Mac Clang it is the same 9.1ms:
alignas(16) uint8_t gathered[16] = {};
for (int lane = 0; lane < 16; ++lane)
{
gathered[lane] = *srcPtr;
srcPtr += channels;
}
uint8x16_t v = vld1q_u8(gathered);
Note that = {}; in variable declaration is important; it’s not enough to just move the variable inside the loop. Logically upon each iteration
the variable is “fresh new variable”, but the compiler decides to not explicitly set that register to zero, thus creating this kinda-false
dependency between loop iterations.
Having the same “written in C” version for the SSE code path still does not result in MSVC emitting SSE instructions though.
Anyway, for compression filter I’m going to call it a day. We are here:
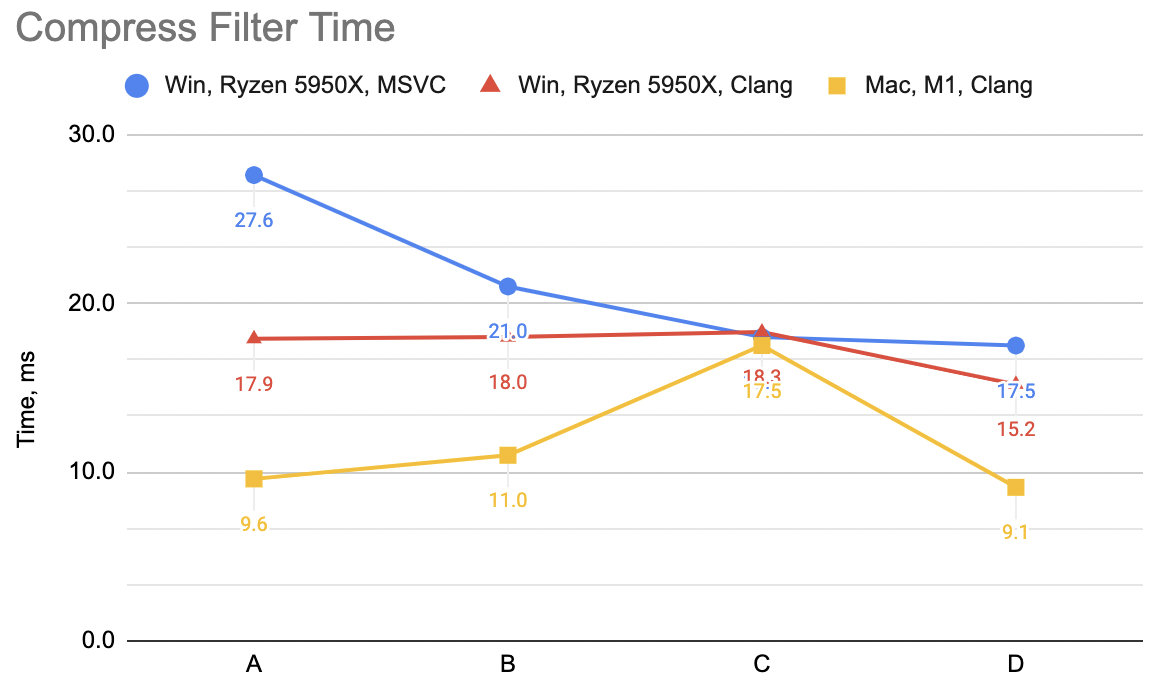
- Good improvement on MSVC,
- A tiny bit of improvement on Clang x64 and ARM. With several regressions along the way, but hey I learned to initialize my registers.
Summary
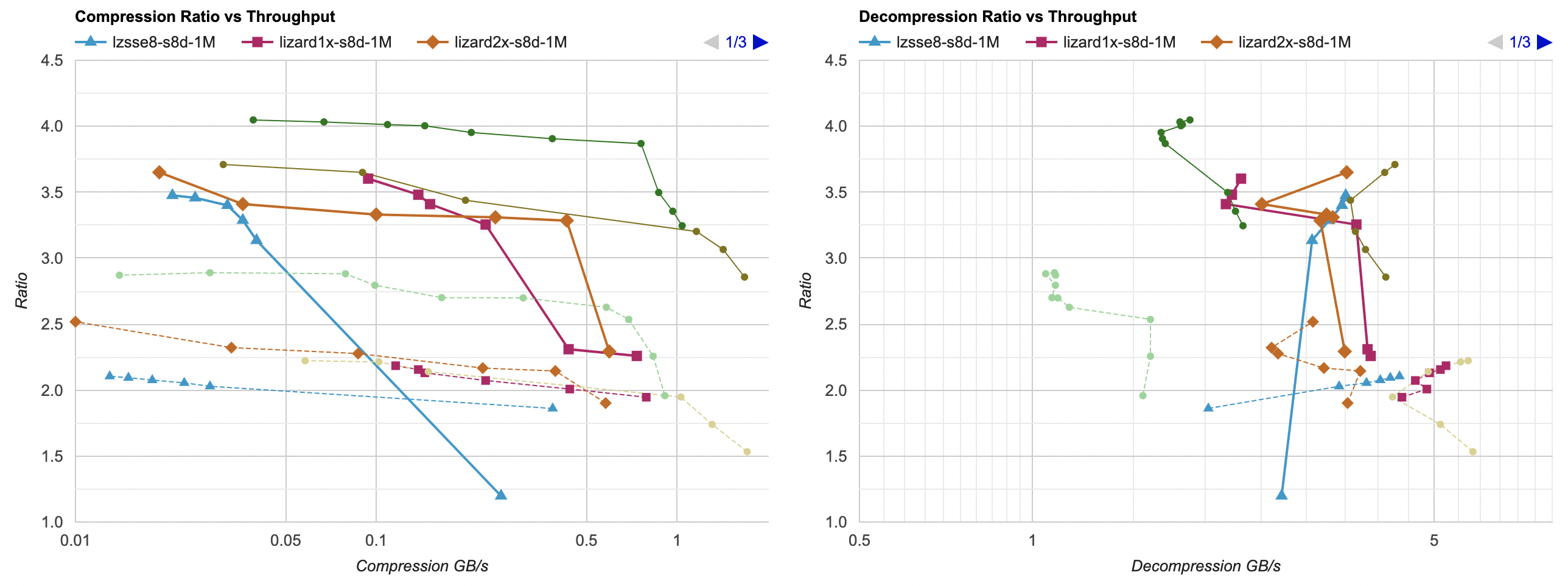
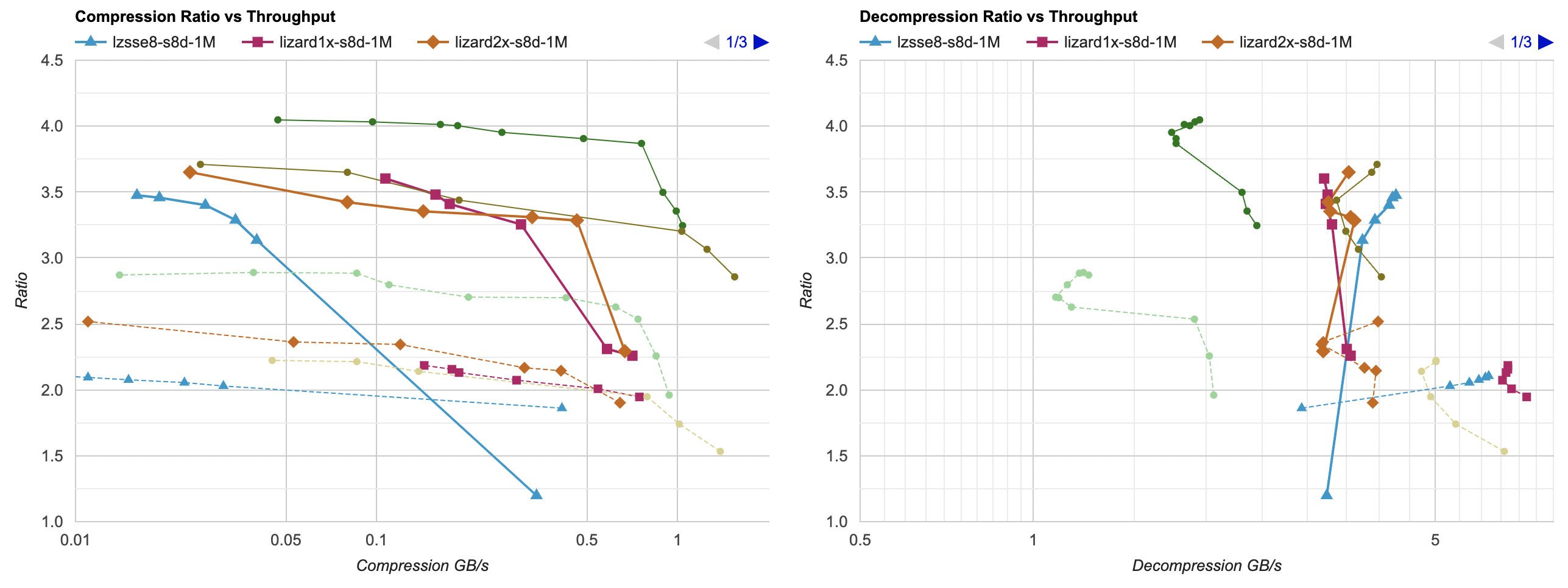
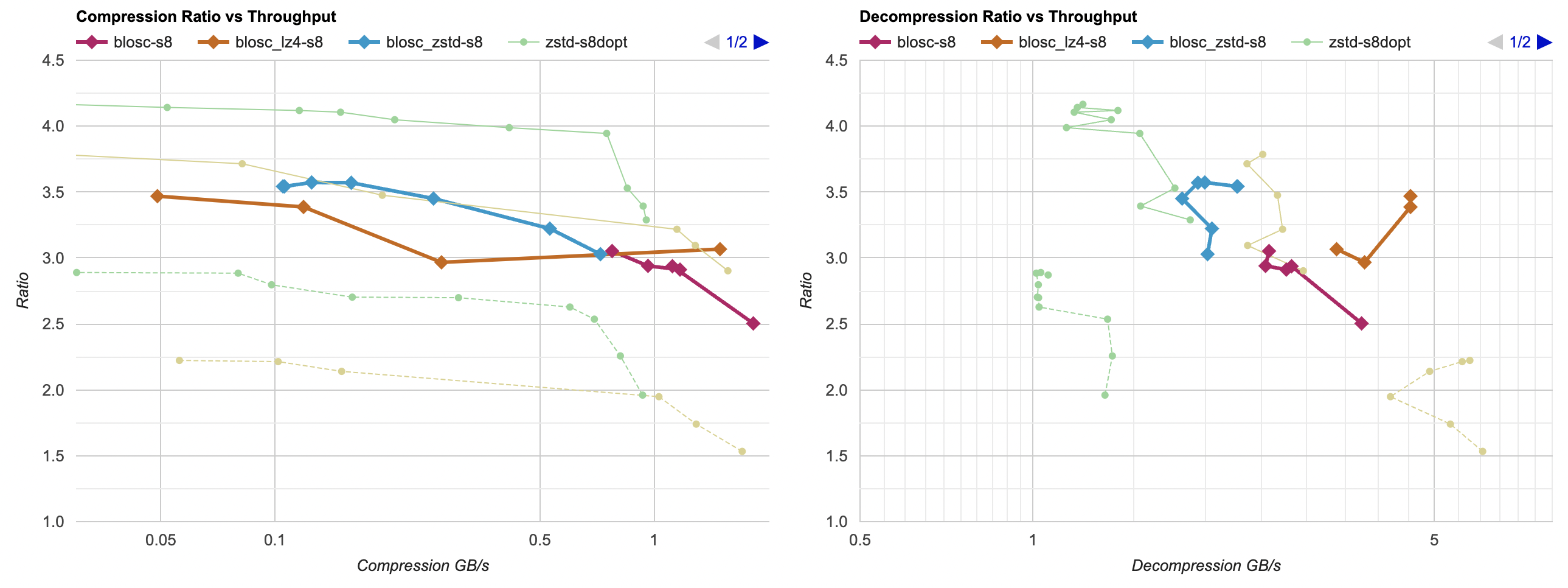
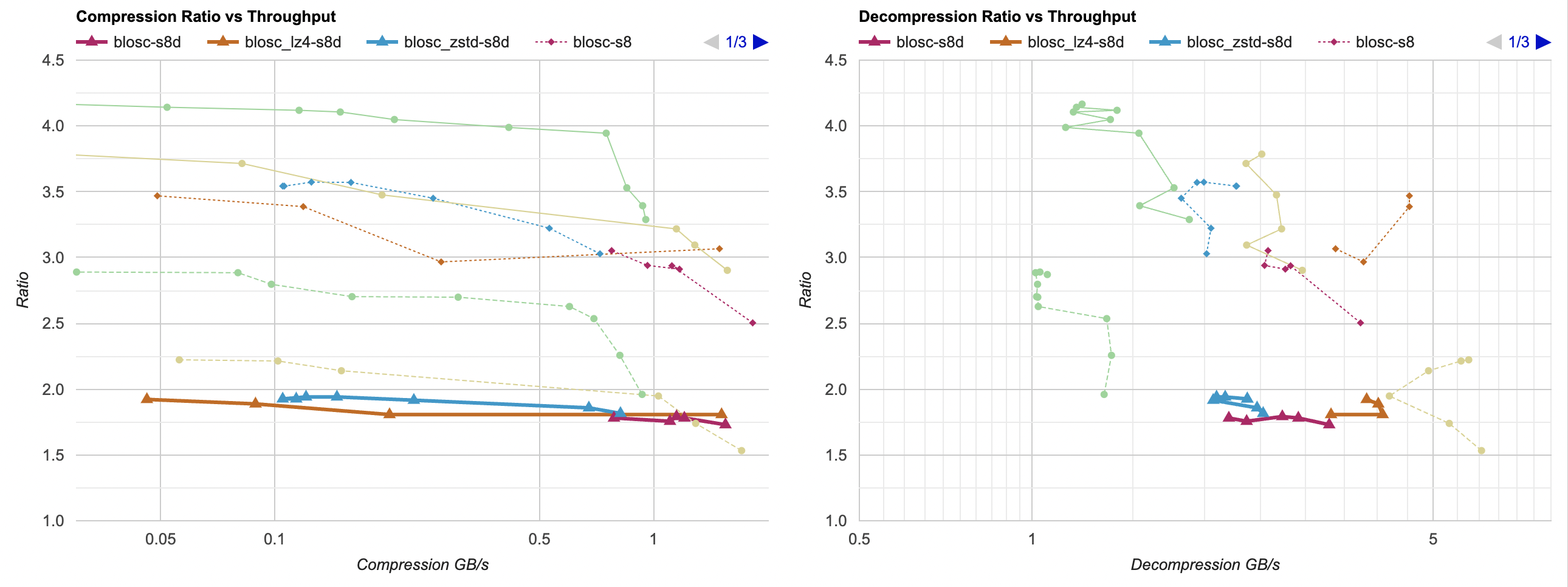
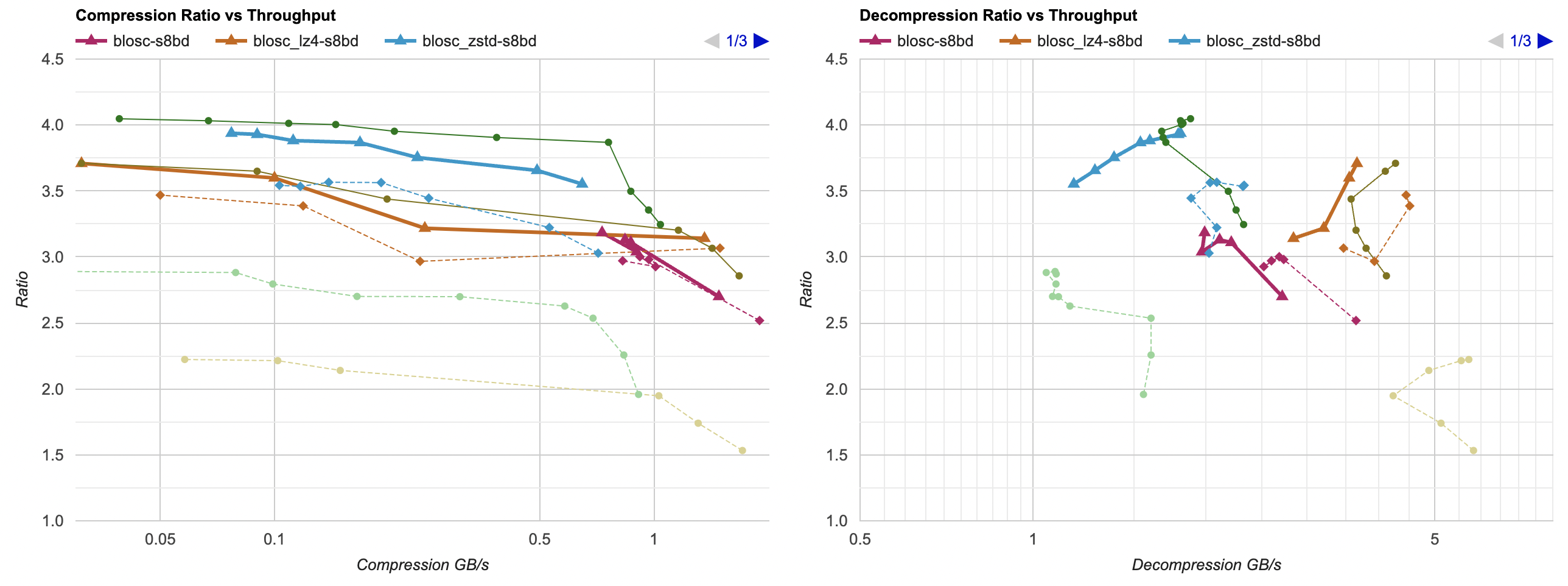
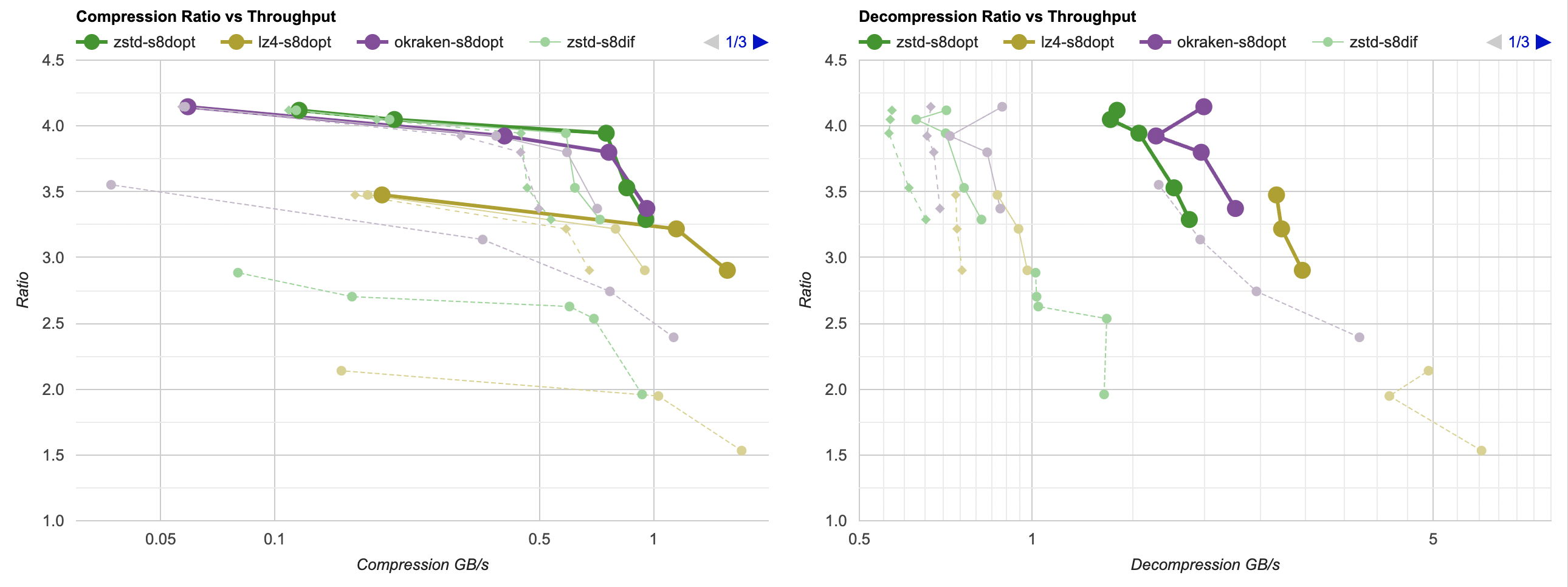
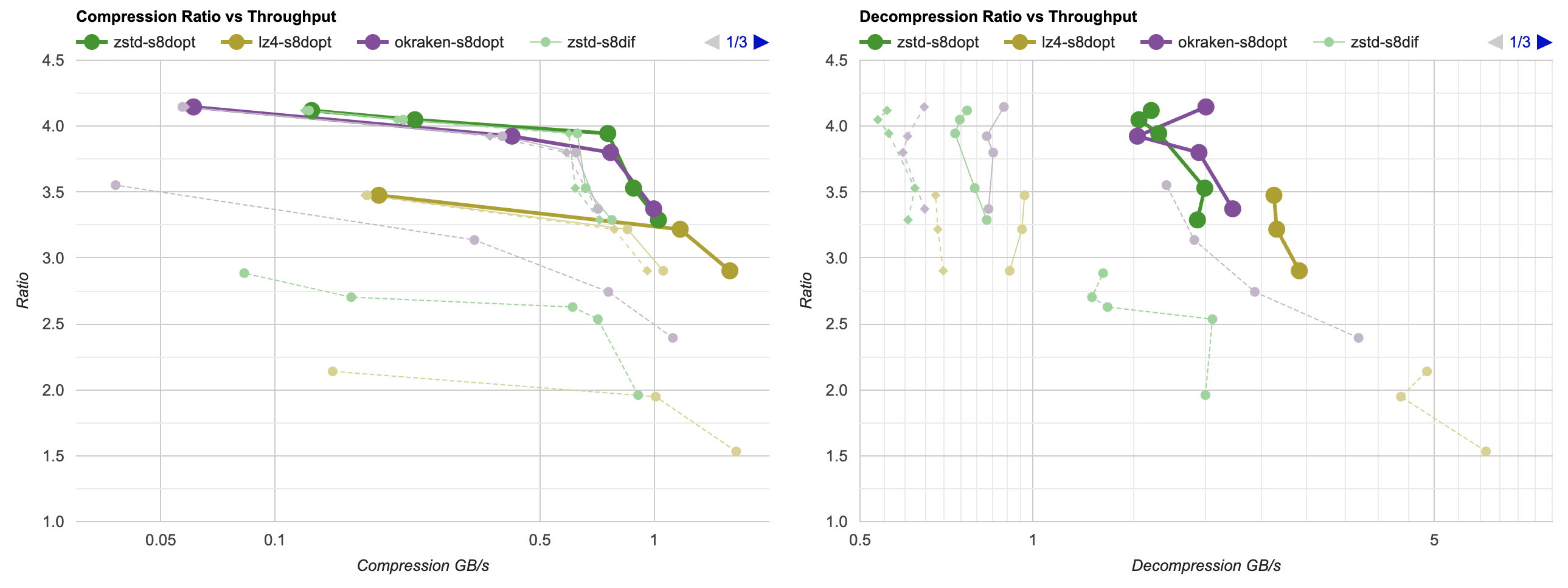
Putting all of that together, here’s how it affects the overall picture. Click for interactive chart; thick line is filter optimized
as above; thin solid line is filter from part 3. Dashed line is just the lossless
compressors, without any data filtering. Windows, Ryzen 5950X, VS2022:
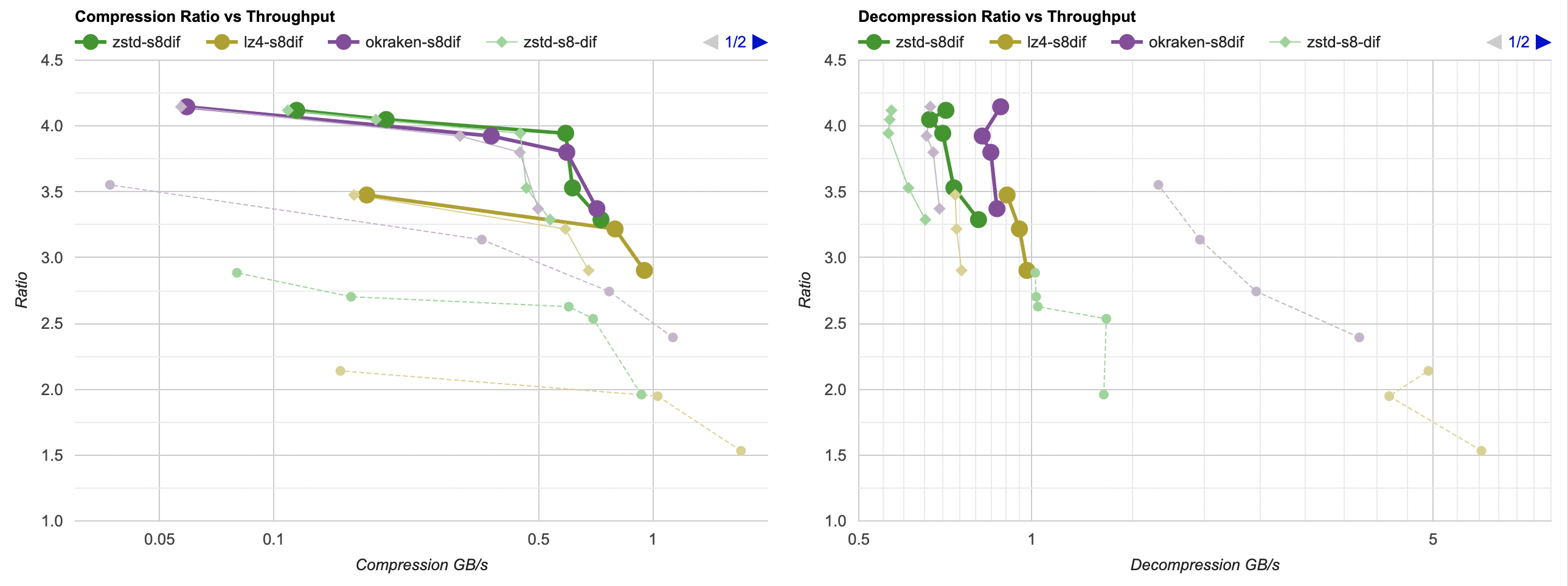
- Compression gets a bit faster; generally saves about 40ms.
- Decompression also gets faster; saves about 30ms but the effect of that is much larger since the decompressors are faster. Something like LZ4
goes from 0.8GB/s to 1.0GB/s. Which is still way below 5GB/s that it does without any data filtering of course, but eh.
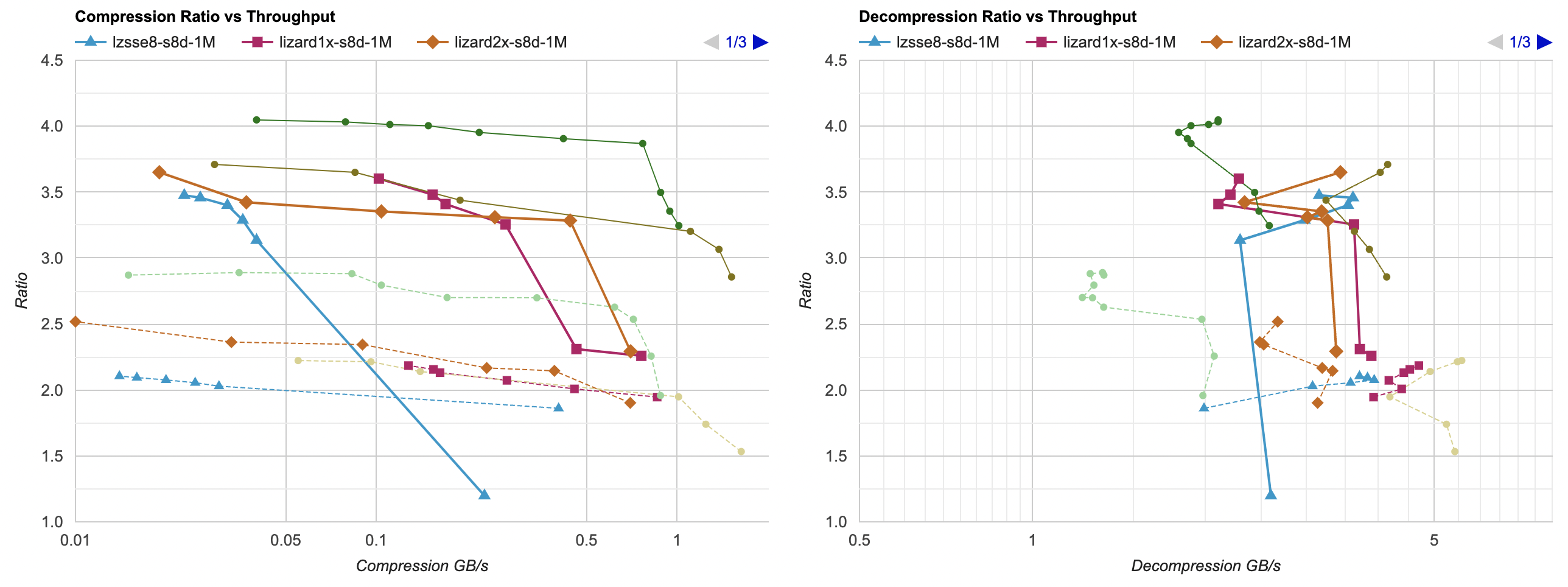
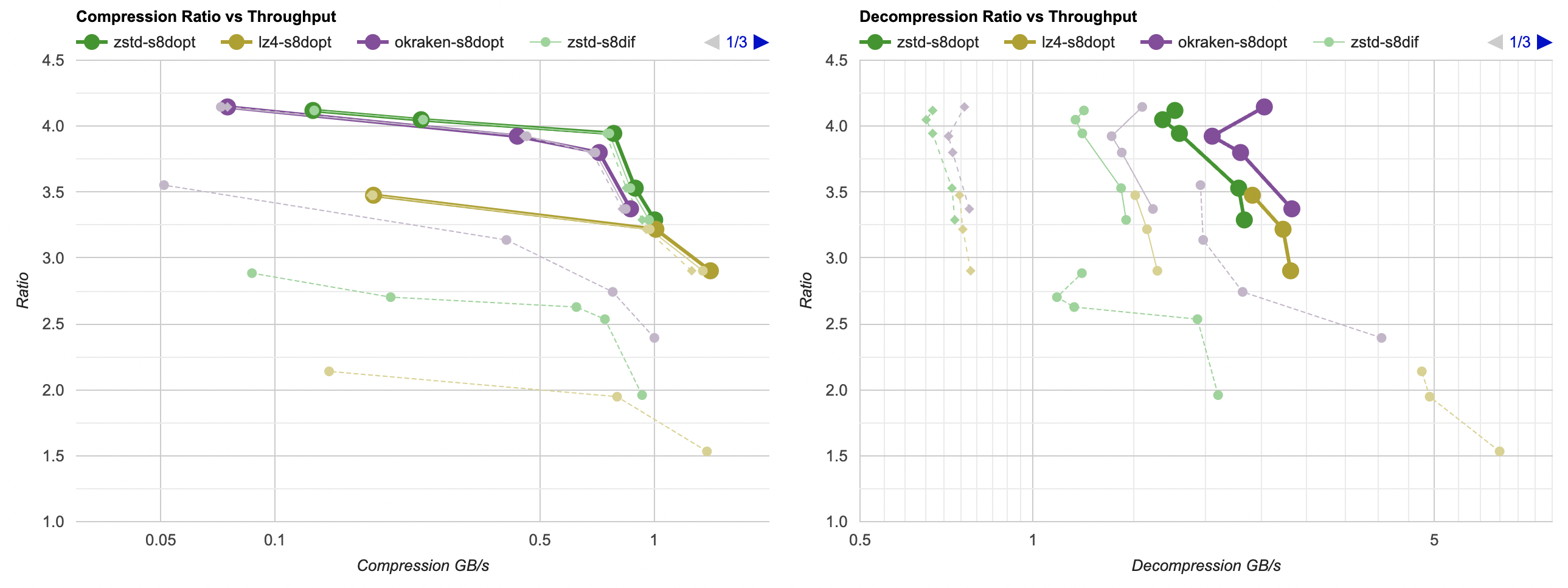
And Mac, Apple M1 Max, Clang 14:
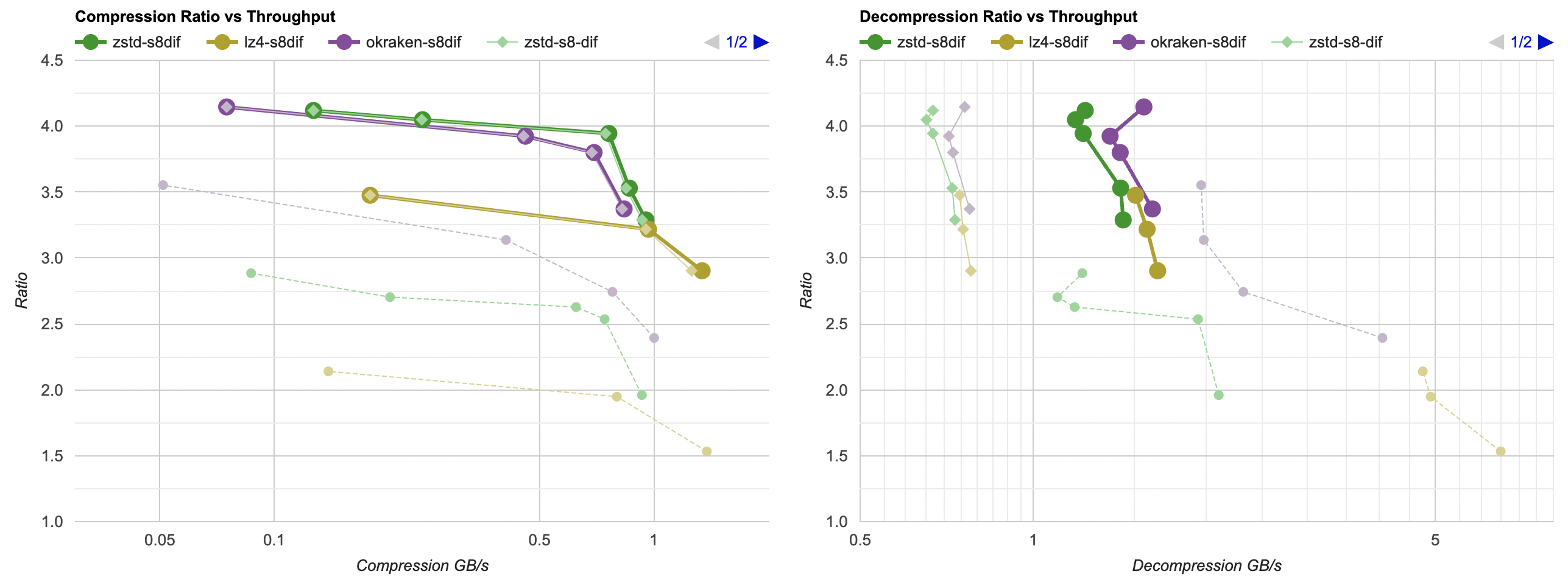
- Compression gets a tiny bit faster, but the effect is so small that it’s really nothing.
- Decompression gets way faster. It saves about 60ms, which gets LZ4 from 0.8GB/s to 1.6GB/s. And for example zstd decompression
now is within same ballpark as without any data filtering!
What’s next
Next up: either look into lossy compression, or into other ways
of speeding up the data filtering.
 What’s a few million badly rendered boxes among friends, anyway?
What’s a few million badly rendered boxes among friends, anyway?